Hausdorff gap
If 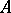 and
and 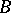 are subsets of
are subsets of 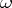 , then one writes
, then one writes 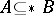 provided that
provided that 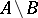 is finite. In addition,
is finite. In addition, 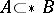 means that
means that  while, moreover,
while, moreover, 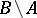 is infinite. Finally,
is infinite. Finally, 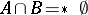 means that
means that 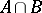 is finite.
is finite.
Let 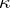 and
and 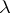 be infinite cardinal numbers (cf. also Cardinal number), and consider the following statement:
be infinite cardinal numbers (cf. also Cardinal number), and consider the following statement:
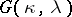 : There are a
: There are a 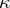 -sequence
-sequence 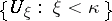 of subsets of
of subsets of 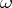 and a
and a  -sequence
-sequence 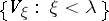 of subsets of
of subsets of 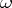 such that:
such that:
1) 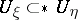 if
if 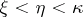 ;
;
2)  if
if 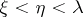 ;
;
3) if 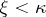 and
and 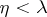 , then
, then 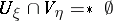 ;
;
4) there does not exist a subset 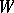 of
of 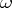 such that
such that 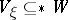 for all
for all 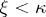 and
and 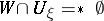 for all
for all 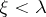 .
.
In [a2], F. Hausdorff proved that 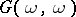 ) is false while
) is false while 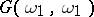 ) is true. The sets that witness the fact that
) is true. The sets that witness the fact that 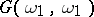 ) holds are called a Hausdorff gap. K. Kunen has shown in [a3] that it is consistent with Martin's axiom (cf. also Suslin hypothesis) and the negation of the continuum hypothesis that
) holds are called a Hausdorff gap. K. Kunen has shown in [a3] that it is consistent with Martin's axiom (cf. also Suslin hypothesis) and the negation of the continuum hypothesis that  ) and
) and 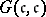 ) both are false. Here,
) both are false. Here,  is the cardinality of the continuum (cf. also Continuum, cardinality of the). He also proved that it is consistent with Martin's axiom and the negation of the continuum hypothesis that
is the cardinality of the continuum (cf. also Continuum, cardinality of the). He also proved that it is consistent with Martin's axiom and the negation of the continuum hypothesis that 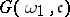 ) and
) and 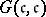 ) both are true. See [a1] for more details.
) both are true. See [a1] for more details.
References
| [a1] | J.E. Baumgartner, "Applications of the Proper Forcing Axiom" K. Kunen (ed.) J.E. Vaughan (ed.) , Handbook of Set Theoretic Topology , North-Holland (1984) pp. 913–959 |
| [a2] | F. Hausdorff, "Summen von 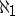 Mengen" Fund. Math. , 26 (1936) pp. 241–255 Mengen" Fund. Math. , 26 (1936) pp. 241–255 |
| [a3] | K. Kunen, "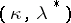 -gaps under MA" Unpublished manuscript -gaps under MA" Unpublished manuscript |
Hausdorff gap. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hausdorff_gap&oldid=13106