Hasse principle
One of the central principles of Diophantine geometry, which reduces the problem of the existence of rational points on an algebraic variety over a global field to the analogous problem over local fields.
Let  be a class of algebraic varieties over a global field
be a class of algebraic varieties over a global field 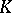 . The Hasse principle holds in
. The Hasse principle holds in  if for any
if for any 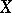 in
in  such that for all non-trivial absolute valuations
such that for all non-trivial absolute valuations  on
on  the set of
the set of 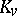 -rational points
-rational points 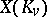 of
of 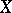 is non-empty, the set of
is non-empty, the set of 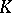 -rational points
-rational points 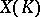 is also not empty (where
is also not empty (where 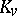 is the completion of
is the completion of 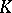 relative to
relative to  ). In particular, if
). In particular, if 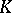 is the field
is the field 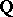 of rational numbers, then if the set of real points
of rational numbers, then if the set of real points  and the set of
and the set of  -adic points
-adic points 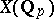 , for all primes
, for all primes 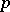 , are not empty, it follows that the set of rational points
, are not empty, it follows that the set of rational points 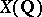 is also not empty. The Hasse principle holds for quadrics [2], and so it is valid for algebraic curves of genus 0 (see [3]). For quadrics over a number field the Hasse principle was stated and proved by H. Hasse in [1]. For cubic hypersurfaces the Hasse principle is not true, in general (see [3], [4]); a counterexample (over
is also not empty. The Hasse principle holds for quadrics [2], and so it is valid for algebraic curves of genus 0 (see [3]). For quadrics over a number field the Hasse principle was stated and proved by H. Hasse in [1]. For cubic hypersurfaces the Hasse principle is not true, in general (see [3], [4]); a counterexample (over 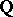 ) is the projective curve
) is the projective curve 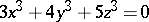 or the projective surface
or the projective surface 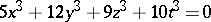 .
.
Let  be an algebraic group over
be an algebraic group over 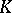 and let
and let 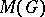 be the class of algebraic varieties consisting of all principal homogeneous spaces over
be the class of algebraic varieties consisting of all principal homogeneous spaces over  (see Galois cohomology; Weil–Châtelet group, and also [2], [3], [5]). One says that the Hasse principle holds for
(see Galois cohomology; Weil–Châtelet group, and also [2], [3], [5]). One says that the Hasse principle holds for  if it holds for
if it holds for 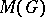 . The Hasse principle holds for simply-connected and adjoint semi-simple algebraic groups over number fields ([5], [6]). If
. The Hasse principle holds for simply-connected and adjoint semi-simple algebraic groups over number fields ([5], [6]). If  is an Abelian variety, then the Hasse principle holds for
is an Abelian variety, then the Hasse principle holds for  if and only if the Shafarevich–Tate group (cf. Galois cohomology) of
if and only if the Shafarevich–Tate group (cf. Galois cohomology) of 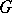 vanishes (see the examples in [7], [8]).
vanishes (see the examples in [7], [8]).
References
| [1] | H. Hasse, "Darstellbarkeit von Zahlen durch quadratische Formen in einem beliebigen algebraischen Zahlkörper" J. Reine Angew. Math. , 153 (1924) pp. 113–130 |
| [2] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1967) |
| [3] | J.W.S. Cassels, "Diophantine equations with special reference to elliptic curves" J. London Math. Soc. , 41 (1966) pp. 193–291 |
| [4] | Yu.I. Manin, "Cubic forms. Algebra, geometry, arithmetic" , North-Holland (1974) (Translated from Russian) |
| [5] | J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964) |
| [6] | V. Chernusov, "The Hasse principle for groups of type 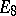 " , Minsk (1988) (In Russian) " , Minsk (1988) (In Russian) |
| [7] | K. Rubin, "Tate–Shafarevich groups and  -functions of elliptic curves with complex multiplication" Invent. Math. , 89 (1987) pp. 527–560 -functions of elliptic curves with complex multiplication" Invent. Math. , 89 (1987) pp. 527–560 |
| [8] | V. Kolyvagin, "The Mordell–Weil groups and the Shafarevich–Tate groups of Weil's elliptic curves" Izv. Akad. Nauk. SSSR Ser. Mat. , 52 : 6 (1988) |
Hasse principle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hasse_principle&oldid=18794