Hartogs domain
From Encyclopedia of Mathematics
semi-circular domain, with symmetry plane 
A domain in the space of  complex variables which, for each point
complex variables which, for each point 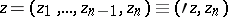 , contains the circle
, contains the circle
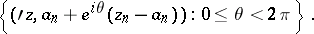 |
Named after F. Hartogs. A Hartogs domain is called complete if for each point 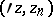 it contains the disc
it contains the disc
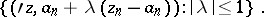 |
A Hartogs domain with symmetry plane 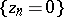 can conveniently be represented by a Hartogs diagram, viz., by the image of the Hartogs domain under the mapping
can conveniently be represented by a Hartogs diagram, viz., by the image of the Hartogs domain under the mapping 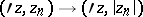 .
.
References
| [1] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
| [2] | S. Bochner, W.T. Martin, "Several complex variables" , Princeton Univ. Press (1948) |
Comments
References
| [a1] | H. Behnke, P. Thullen, "Theorie der Funktionen meherer komplexer Veränderlichen" , Springer (1970) (Elraged & Revised Edition. Original: 1934) |
How to Cite This Entry:
Hartogs domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hartogs_domain&oldid=15532
Hartogs domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hartogs_domain&oldid=15532
This article was adapted from an original article by E.M. Chirka (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article