Harnack theorem
Harnack's first theorem: If a sequence of functions which are harmonic in a bounded domain 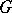 and continuous on
and continuous on 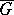 converges uniformly on the boundary
converges uniformly on the boundary 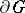 , then it also converges uniformly in
, then it also converges uniformly in 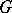 to a harmonic function. This theorem can be generalized to solutions of an elliptic equation,
to a harmonic function. This theorem can be generalized to solutions of an elliptic equation,
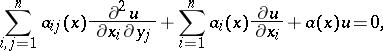 | (*) |
which has a unique solution of the Dirichlet problem for any continuous boundary function . If the sequence of solutions of equation (*) converges uniformly on 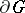 , then it also converges uniformly in
, then it also converges uniformly in 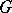 to a solution of equation (*).
to a solution of equation (*).
Harnack's second theorem, the Harnack principle: If a monotone sequence of harmonic functions in a bounded domain 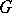 converges at some point in
converges at some point in 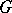 , then it converges at all points of
, then it converges at all points of  to a harmonic function, and this convergence is uniform on any closed subdomain of
to a harmonic function, and this convergence is uniform on any closed subdomain of  . Harnack's second theorem can be generalized to monotone sequences of solutions of the elliptic equation .
. Harnack's second theorem can be generalized to monotone sequences of solutions of the elliptic equation .
References
| [1] | I.G. [I.G. Petrovskii] Petrowski, "Vorlesungen über partielle Differentialgleichungen" , Teubner (1965) (Translated from Russian) |
| [2] | A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) |
Comments
In the axiomatic theory of harmonic spaces (cf. Harmonic space) the first Harnack theorem is known as the Bauer convergence property and the second Harnack theorem as the Brélot convergence property, see [a3] and [a1]. The following properties are equivalent to the Brélot convergence property (see [a4]): 1) each positive harmonic function  on a domain
on a domain 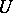 is either strictly positive or
is either strictly positive or 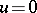 . Moreover, the set of positive harmonic functions on
. Moreover, the set of positive harmonic functions on 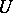 , equal to 1 in a given point
, equal to 1 in a given point 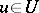 , is equicontinuous (cf. Equicontinuity); and 2) for any domain
, is equicontinuous (cf. Equicontinuity); and 2) for any domain  and any compact subset
and any compact subset 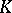 of
of 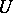 there exists a constant
there exists a constant 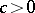 such that
such that 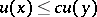 for any
for any 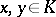 and any positive harmonic function
and any positive harmonic function  on
on 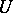 (the Harnack inequality).
(the Harnack inequality).
References
| [a1] | J.-M. Bony, "Opérateurs elliptiques dégénérés associés aux axiomatiques de la théorie du potentiel" M. Brelot (ed.) H. Bauer (ed.) J.-M. Bony (ed.) J. Deny (ed.) G. Mokobodzki (ed.) , Potential theory (CIME, Stresa, 1969) , Cremonese (1970) pp. 69–119 |
| [a2] | M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959) |
| [a3] | C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972) |
| [a4] | P. Loeb, B. Walsh, "The equivalence of Harnack's principle and Harnack's inequality in the axiomatic system of Brélot" Ann. Inst. Fourier , 15 : 2 (1965) pp. 597–600 |
Harnack theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Harnack_theorem&oldid=17463