Difference between revisions of "Harnack inequality"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | h0466001.png | ||
| + | $#A+1 = 69 n = 0 | ||
| + | $#C+1 = 69 : ~/encyclopedia/old_files/data/H046/H.0406600 Harnack inequality | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''(dual Harnack inequality)'' | ''(dual Harnack inequality)'' | ||
| − | An inequality that gives an estimate from above and an estimate from below for the ratio | + | An inequality that gives an estimate from above and an estimate from below for the ratio $ u( x)/u( y) $ |
| + | of two values of a positive harmonic function; obtained by A. Harnack [[#References|[1]]]. Let $ u \geq 0 $ | ||
| + | be a harmonic function in a domain $ G $ | ||
| + | of an $ n $- | ||
| + | dimensional Euclidean space; let $ E _ {r} ( y) $ | ||
| + | be the ball $ \{ {x } : {| x - y | < r } \} $ | ||
| + | with radius $ r $ | ||
| + | and centre at the point $ y $. | ||
| + | If the closure $ \overline{ {E _ {r} ( y) }}\; \subset G $, | ||
| + | then the Harnack inequality | ||
| + | |||
| + | $$ \tag{1 } | ||
| + | \left ( { | ||
| + | \frac{r}{r + \rho } | ||
| + | } \right ) ^ {n - 2 } | ||
| − | + | \frac{r - \rho }{r + \rho } | |
| + | |||
| + | u ( y) \leq u ( x) \leq \ | ||
| + | \left ( { | ||
| + | \frac{r}{r - \rho } | ||
| + | } \right ) ^ {n - 2 } | ||
| + | |||
| + | \frac{r + \rho }{r - \rho } | ||
| + | u ( y) , | ||
| + | $$ | ||
or | or | ||
| − | + | $$ | |
| + | \max _ {x \in E _ \rho ( y) } \ | ||
| + | u ( x) \leq \left ( | ||
| − | + | \frac{r + \rho }{r - \rho } | |
| + | \right ) ^ {n} \ | ||
| + | \min _ {x \in E _ \rho ( y) } u ( x), | ||
| + | $$ | ||
| − | < | + | is valid for all $ x \in E _ \rho ( y) $, |
| + | $ 0 \leq \rho < r $. | ||
| + | If $ g $ | ||
| + | is a compactum, $ \overline{g}\; \subset G $, | ||
| + | then there exists a number $ M = M( G, g) $ | ||
| + | such that | ||
| − | + | $$ \tag{2 } | |
| + | M ^ {-} 1 u ( y) \leq u ( x) \leq Mu ( y) | ||
| + | $$ | ||
| − | + | for any $ x, y \in \overline{g}\; $. | |
| + | In particular, | ||
| + | |||
| + | $$ | ||
| + | \max _ {x \in g } u ( x) \leq \ | ||
| + | M \min _ {x \in g } u ( x). | ||
| + | $$ | ||
Harnack's inequality has the following corollaries: the strong [[Maximum principle|maximum principle]], the [[Harnack theorem|Harnack theorem]] on sequences of harmonic functions, compactness theorems for families of harmonic functions, the Liouville theorem (cf. [[Liouville theorems|Liouville theorems]]), and other facts. Harnack's inequality can be generalized [[#References|[3]]], [[#References|[4]]] to non-negative solutions of a wide class of linear elliptic equations of the form | Harnack's inequality has the following corollaries: the strong [[Maximum principle|maximum principle]], the [[Harnack theorem|Harnack theorem]] on sequences of harmonic functions, compactness theorems for families of harmonic functions, the Liouville theorem (cf. [[Liouville theorems|Liouville theorems]]), and other facts. Harnack's inequality can be generalized [[#References|[3]]], [[#References|[4]]] to non-negative solutions of a wide class of linear elliptic equations of the form | ||
| − | + | $$ | |
| + | Lu \equiv \ | ||
| + | \sum _ {i, j = 1 } ^ { n } | ||
| + | { | ||
| + | \frac \partial {\partial x ^ {i} } | ||
| + | } | ||
| + | \left ( a ^ {ij} ( x) | ||
| + | |||
| + | \frac{\partial u }{\partial x ^ {j} } | ||
| + | |||
| + | \right ) + | ||
| + | \sum _ {i = 1 } ^ { n } | ||
| + | b ^ {i} ( x) | ||
| + | |||
| + | \frac{\partial u }{\partial x ^ {i} } | ||
| + | + | ||
| + | c ( x) u = 0 | ||
| + | $$ | ||
| − | with a uniformly positive-definite matrix | + | with a uniformly positive-definite matrix $ \| a ^ {ij} \| $: |
| − | + | $$ | |
| + | \lambda \sum _ {i = 1 } ^ { n } | ||
| + | \xi _ {i} ^ {2} \leq \ | ||
| + | \sum _ {i, j = 1 } ^ { n } | ||
| + | a ^ {ij} ( x) \xi _ {i} \xi _ {j} \leq \ | ||
| + | \Lambda \sum _ {i = 1 } ^ { n } \xi _ {i} ^ {2} , | ||
| + | $$ | ||
| − | where | + | where $ \Lambda \geq \lambda > 0 $ |
| + | are numbers, $ \xi = ( \xi _ {1} \dots \xi _ {n} ) $ | ||
| + | is any $ n $- | ||
| + | dimensional vector and $ x \in G $. | ||
| + | The constant $ M $ | ||
| + | in inequality (2) depends only on $ \lambda $, | ||
| + | $ \Lambda $, | ||
| + | certain norms of the lower coefficients of the operator $ L $, | ||
| + | and the distance between the boundaries of $ G $ | ||
| + | and of $ g $. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/h046600a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/h046600a.gif" /> | ||
| Line 31: | Line 116: | ||
Figure: h046600a | Figure: h046600a | ||
| − | The analogue of Harnack's inequality is also applicable [[#References|[5]]] to non-negative solutions | + | The analogue of Harnack's inequality is also applicable [[#References|[5]]] to non-negative solutions $ u( x, t) $ |
| + | of uniformly-parabolic equations of the form $ u _ {t} + Lu= 0 $( | ||
| + | the coefficients of the operator $ L $ | ||
| + | may also depend on $ t $). | ||
| + | In such a case only a one-sided inequality | ||
| + | |||
| + | $$ | ||
| + | u ( x, t) \leq Mu ( y, \tau ) | ||
| + | $$ | ||
| − | + | is possible for points $ ( x, t) $ | |
| + | lying inside the paraboloid | ||
| − | + | $$ | |
| + | \{ {( x, t) } : {| x - y | ^ {2} \leq | ||
| + | \mu ^ {2} ( \tau - t),\ | ||
| + | \tau - v ^ {2} \leq t \leq \tau } \} | ||
| + | , | ||
| + | $$ | ||
| − | + | which is concave downwards with apex at $ ( y, \tau ) $( | |
| + | Fig., left part). Here $ M $ | ||
| + | depends on $ y $, | ||
| + | $ \tau $, | ||
| + | $ \lambda $, | ||
| + | $ \Lambda $, | ||
| + | $ \mu $, | ||
| + | $ \nu $, | ||
| + | on certain norms of the lower coefficients of the operator $ L $, | ||
| + | and on the distance between the boundary of the paraboloid and the boundary of the domain on which $ u \geq 0 $. | ||
| + | If, for instance, $ u \geq 0 $ | ||
| + | in the cylinder | ||
| − | + | $$ | |
| + | Q = G \times ( a, b],\ \ | ||
| + | \overline{g}\; \subset G, | ||
| + | $$ | ||
| − | + | if the distance between $ \partial G $ | |
| + | and $ \partial g $ | ||
| + | is at least $ d > 0 $ | ||
| + | and if $ d $ | ||
| + | is sufficiently small, then the inequality [[#References|[5]]] | ||
| − | + | $$ | |
| + | \mathop{\rm ln} | ||
| + | \frac{u ( x, t) }{u ( y, \tau ) } | ||
| − | + | \leq M \left ( | |
| − | + | \frac{| x - y | ^ {2} }{\tau - t } | |
| + | + | ||
| − | + | \frac{\tau - t }{d ^ {2} } | |
| + | + | ||
| + | 1 \right ) | ||
| + | $$ | ||
| + | |||
| + | is valid in $ g \times ( a - d ^ {2} , b ] $. | ||
| + | In particular, if $ u \geq 0 $ | ||
| + | in $ Q $( | ||
| + | Fig., right part), if the compacta $ Q _ {1} $ | ||
| + | and $ Q _ {2} $ | ||
| + | are situated in $ Q $ | ||
| + | and if | ||
| + | |||
| + | $$ | ||
| + | \delta = \ | ||
| + | \min _ {\begin{array}{c} | ||
| + | ( x, t) \in Q _ {1} , \\ | ||
| + | ( y, \tau ) \in Q _ {2} | ||
| + | \end{array} | ||
| + | } \ | ||
| + | ( t - \tau ) > 0, | ||
| + | $$ | ||
then | then | ||
| − | + | $$ | |
| + | \max _ {( x, t) \in Q _ {2} } u ( x, t) \leq M \ | ||
| + | \min _ {( x, t) \in Q _ {1} } u ( x, t), | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | M = M ( \delta , Q, Q _ {1} , Q _ {2} , L). | ||
| + | $$ | ||
The example of the function | The example of the function | ||
| − | + | $$ | |
| + | u ( x, t) = \mathop{\rm exp} \left ( | ||
| + | \sum _ {i = 1 } ^ { n } | ||
| + | k _ {i} x ^ {i} + t | ||
| + | \sum _ {i = 1 } ^ { n } | ||
| + | k _ {i} ^ {2} \right ) , | ||
| + | $$ | ||
| − | which is a solution of the heat equation | + | which is a solution of the heat equation $ u _ {t} - \Delta u = 0 $ |
| + | for any $ k _ {1} \dots k _ {n} $, | ||
| + | shows that in the parabolic case it is impossible to have two-sided estimates. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Harnack, "Die Grundlagen der Theorie des logarithmischen Potentiales und der eindeutigen Potentialfunktion in der Ebene" , Leipzig (1887) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , '''2''' , Interscience (1965) (Translated from German) {{MR|0195654}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Serrin, "On the Harnack inequality for linear elliptic equations" ''J. d'Anal. Math.'' , '''4''' : 2 (1955–1956) pp. 292–308 {{MR|0081415}} {{ZBL|0070.32302}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J. Moser, "On Harnack's theorem for elliptic differential equations" ''Comm. Pure Appl. Math.'' , '''14''' (1961) pp. 577–591 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J. Moser, "On Harnack's theorem for parabolic differential equations" ''Comm. Pure Appl. Math.'' , '''17''' (1964) pp. 101–134 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) {{MR|0181836}} {{ZBL|0144.34903}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> E.M. Landis, "Second-order equations of elliptic and parabolic type" , Moscow (1971) (In Russian) {{MR|0320507}} {{ZBL|0226.35001}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Harnack, "Die Grundlagen der Theorie des logarithmischen Potentiales und der eindeutigen Potentialfunktion in der Ebene" , Leipzig (1887) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , '''2''' , Interscience (1965) (Translated from German) {{MR|0195654}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Serrin, "On the Harnack inequality for linear elliptic equations" ''J. d'Anal. Math.'' , '''4''' : 2 (1955–1956) pp. 292–308 {{MR|0081415}} {{ZBL|0070.32302}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J. Moser, "On Harnack's theorem for elliptic differential equations" ''Comm. Pure Appl. Math.'' , '''14''' (1961) pp. 577–591 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J. Moser, "On Harnack's theorem for parabolic differential equations" ''Comm. Pure Appl. Math.'' , '''17''' (1964) pp. 101–134 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) {{MR|0181836}} {{ZBL|0144.34903}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> E.M. Landis, "Second-order equations of elliptic and parabolic type" , Moscow (1971) (In Russian) {{MR|0320507}} {{ZBL|0226.35001}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | See [[#References|[a2]]] for a Harnack inequality up to the boundary of | + | See [[#References|[a2]]] for a Harnack inequality up to the boundary of $ G $. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N. Boboc, P. Mustaţă, "Espaces harmoniques associés aux opérateurs différentiels linéaires du second order de type elliptique" , Springer (1968) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L.L. Helms, "Introduction to potential theory" , Wiley (Interscience) (1969)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N. Boboc, P. Mustaţă, "Espaces harmoniques associés aux opérateurs différentiels linéaires du second order de type elliptique" , Springer (1968) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L.L. Helms, "Introduction to potential theory" , Wiley (Interscience) (1969)</TD></TR></table> | ||
Latest revision as of 19:43, 5 June 2020
(dual Harnack inequality)
An inequality that gives an estimate from above and an estimate from below for the ratio $ u( x)/u( y) $ of two values of a positive harmonic function; obtained by A. Harnack [1]. Let $ u \geq 0 $ be a harmonic function in a domain $ G $ of an $ n $- dimensional Euclidean space; let $ E _ {r} ( y) $ be the ball $ \{ {x } : {| x - y | < r } \} $ with radius $ r $ and centre at the point $ y $. If the closure $ \overline{ {E _ {r} ( y) }}\; \subset G $, then the Harnack inequality
$$ \tag{1 } \left ( { \frac{r}{r + \rho } } \right ) ^ {n - 2 } \frac{r - \rho }{r + \rho } u ( y) \leq u ( x) \leq \ \left ( { \frac{r}{r - \rho } } \right ) ^ {n - 2 } \frac{r + \rho }{r - \rho } u ( y) , $$
or
$$ \max _ {x \in E _ \rho ( y) } \ u ( x) \leq \left ( \frac{r + \rho }{r - \rho } \right ) ^ {n} \ \min _ {x \in E _ \rho ( y) } u ( x), $$
is valid for all $ x \in E _ \rho ( y) $, $ 0 \leq \rho < r $. If $ g $ is a compactum, $ \overline{g}\; \subset G $, then there exists a number $ M = M( G, g) $ such that
$$ \tag{2 } M ^ {-} 1 u ( y) \leq u ( x) \leq Mu ( y) $$
for any $ x, y \in \overline{g}\; $. In particular,
$$ \max _ {x \in g } u ( x) \leq \ M \min _ {x \in g } u ( x). $$
Harnack's inequality has the following corollaries: the strong maximum principle, the Harnack theorem on sequences of harmonic functions, compactness theorems for families of harmonic functions, the Liouville theorem (cf. Liouville theorems), and other facts. Harnack's inequality can be generalized [3], [4] to non-negative solutions of a wide class of linear elliptic equations of the form
$$ Lu \equiv \ \sum _ {i, j = 1 } ^ { n } { \frac \partial {\partial x ^ {i} } } \left ( a ^ {ij} ( x) \frac{\partial u }{\partial x ^ {j} } \right ) + \sum _ {i = 1 } ^ { n } b ^ {i} ( x) \frac{\partial u }{\partial x ^ {i} } + c ( x) u = 0 $$
with a uniformly positive-definite matrix $ \| a ^ {ij} \| $:
$$ \lambda \sum _ {i = 1 } ^ { n } \xi _ {i} ^ {2} \leq \ \sum _ {i, j = 1 } ^ { n } a ^ {ij} ( x) \xi _ {i} \xi _ {j} \leq \ \Lambda \sum _ {i = 1 } ^ { n } \xi _ {i} ^ {2} , $$
where $ \Lambda \geq \lambda > 0 $ are numbers, $ \xi = ( \xi _ {1} \dots \xi _ {n} ) $ is any $ n $- dimensional vector and $ x \in G $. The constant $ M $ in inequality (2) depends only on $ \lambda $, $ \Lambda $, certain norms of the lower coefficients of the operator $ L $, and the distance between the boundaries of $ G $ and of $ g $.
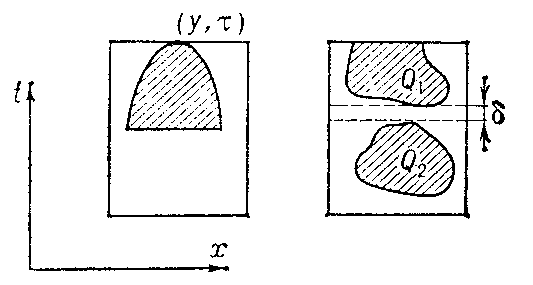
Figure: h046600a
The analogue of Harnack's inequality is also applicable [5] to non-negative solutions $ u( x, t) $ of uniformly-parabolic equations of the form $ u _ {t} + Lu= 0 $( the coefficients of the operator $ L $ may also depend on $ t $). In such a case only a one-sided inequality
$$ u ( x, t) \leq Mu ( y, \tau ) $$
is possible for points $ ( x, t) $ lying inside the paraboloid
$$ \{ {( x, t) } : {| x - y | ^ {2} \leq \mu ^ {2} ( \tau - t),\ \tau - v ^ {2} \leq t \leq \tau } \} , $$
which is concave downwards with apex at $ ( y, \tau ) $( Fig., left part). Here $ M $ depends on $ y $, $ \tau $, $ \lambda $, $ \Lambda $, $ \mu $, $ \nu $, on certain norms of the lower coefficients of the operator $ L $, and on the distance between the boundary of the paraboloid and the boundary of the domain on which $ u \geq 0 $. If, for instance, $ u \geq 0 $ in the cylinder
$$ Q = G \times ( a, b],\ \ \overline{g}\; \subset G, $$
if the distance between $ \partial G $ and $ \partial g $ is at least $ d > 0 $ and if $ d $ is sufficiently small, then the inequality [5]
$$ \mathop{\rm ln} \frac{u ( x, t) }{u ( y, \tau ) } \leq M \left ( \frac{| x - y | ^ {2} }{\tau - t } + \frac{\tau - t }{d ^ {2} } + 1 \right ) $$
is valid in $ g \times ( a - d ^ {2} , b ] $. In particular, if $ u \geq 0 $ in $ Q $( Fig., right part), if the compacta $ Q _ {1} $ and $ Q _ {2} $ are situated in $ Q $ and if
$$ \delta = \ \min _ {\begin{array}{c} ( x, t) \in Q _ {1} , \\ ( y, \tau ) \in Q _ {2} \end{array} } \ ( t - \tau ) > 0, $$
then
$$ \max _ {( x, t) \in Q _ {2} } u ( x, t) \leq M \ \min _ {( x, t) \in Q _ {1} } u ( x, t), $$
where
$$ M = M ( \delta , Q, Q _ {1} , Q _ {2} , L). $$
The example of the function
$$ u ( x, t) = \mathop{\rm exp} \left ( \sum _ {i = 1 } ^ { n } k _ {i} x ^ {i} + t \sum _ {i = 1 } ^ { n } k _ {i} ^ {2} \right ) , $$
which is a solution of the heat equation $ u _ {t} - \Delta u = 0 $ for any $ k _ {1} \dots k _ {n} $, shows that in the parabolic case it is impossible to have two-sided estimates.
References
| [1] | A. Harnack, "Die Grundlagen der Theorie des logarithmischen Potentiales und der eindeutigen Potentialfunktion in der Ebene" , Leipzig (1887) |
| [2] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) MR0195654 |
| [3] | J. Serrin, "On the Harnack inequality for linear elliptic equations" J. d'Anal. Math. , 4 : 2 (1955–1956) pp. 292–308 MR0081415 Zbl 0070.32302 |
| [4] | J. Moser, "On Harnack's theorem for elliptic differential equations" Comm. Pure Appl. Math. , 14 (1961) pp. 577–591 |
| [5] | J. Moser, "On Harnack's theorem for parabolic differential equations" Comm. Pure Appl. Math. , 17 (1964) pp. 101–134 |
| [6] | A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) MR0181836 Zbl 0144.34903 |
| [7] | E.M. Landis, "Second-order equations of elliptic and parabolic type" , Moscow (1971) (In Russian) MR0320507 Zbl 0226.35001 |
Comments
See [a2] for a Harnack inequality up to the boundary of $ G $.
References
| [a1] | N. Boboc, P. Mustaţă, "Espaces harmoniques associés aux opérateurs différentiels linéaires du second order de type elliptique" , Springer (1968) |
| [a2] | L.L. Helms, "Introduction to potential theory" , Wiley (Interscience) (1969) |
Harnack inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Harnack_inequality&oldid=28213