Harmonics
The simplest periodic functions of the form
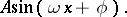 |
These functions are encountered in the study of many oscillatory processes. The number  is known as the amplitude,
is known as the amplitude,  is known as the frequency,
is known as the frequency,  is known as the initial phase, and
is known as the initial phase, and  is the oscillation period. The functions
is the oscillation period. The functions  are, respectively, the second, third, etc., higher harmonics with respect to the fundamental harmonic. In addition to the harmonics themselves, their sums
are, respectively, the second, third, etc., higher harmonics with respect to the fundamental harmonic. In addition to the harmonics themselves, their sums
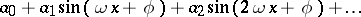 | (*) |
are also considered, since a very broad class of functions can be expanded in series of the form (*) in the study of various processes.
Comments
More generally, if  is a compact group,
is a compact group,  is a closed subgroup of
is a closed subgroup of  and if the regular representation of
and if the regular representation of 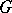 on
on  decomposes uniquely into irreducible subrepresentations, then the functions on the homogeneous space
decomposes uniquely into irreducible subrepresentations, then the functions on the homogeneous space  belonging to irreducible subspaces of
belonging to irreducible subspaces of 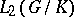 are called harmonics, cf. [a1]. For
are called harmonics, cf. [a1]. For 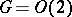 ,
, 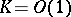 , one finds the classical harmonics.
, one finds the classical harmonics.
References
| [a1] | H. Weyl, "Harmonics on homogeneous manifolds" Ann. of Math. , 35 (1934) pp. 486–499 |
| [a2] | E.W. Hobson, "The theory of spherical and ellipsoidal harmonics" , Chelsea, reprint (1955) |
Harmonics. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Harmonics&oldid=11587