Harmonic quadruple
of points
A quadruple of points on a straight line with cross ratio equal to  . If
. If  is a harmonic quadruple of points, one says that the pair
is a harmonic quadruple of points, one says that the pair  harmonically divides the pair
harmonically divides the pair  , or that the points
, or that the points  and
and  are harmonically conjugate with respect to the points
are harmonically conjugate with respect to the points  and
and  ; the pairs
; the pairs  and
and 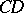 are called harmonically conjugate.
are called harmonically conjugate.

Figure: h046530a
A harmonic quadruple can be defined without recourse to metric concepts. Let 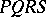 be a quadrangle (see Fig.), let
be a quadrangle (see Fig.), let 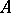 and
and  be the intersection points of the opposite sides, and let
be the intersection points of the opposite sides, and let 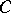 and
and 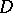 be the intersection points of the diagonals
be the intersection points of the diagonals  and
and 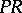 of
of 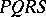 with the straight line
with the straight line 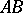 . Then the quadruple of points
. Then the quadruple of points 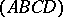 is a harmonic quadruple. A quadruple of straight lines (or planes) passing through a single point (a single straight line) is called a harmonic quadruple of straight lines (planes) if a straight line intersects it in a harmonic quadruple of points.
is a harmonic quadruple. A quadruple of straight lines (or planes) passing through a single point (a single straight line) is called a harmonic quadruple of straight lines (planes) if a straight line intersects it in a harmonic quadruple of points.
Comments
When the straight line is a complex one, but viewed as a Euclidean plane, one says harmonic quadrilateral, see [a1].
For example, use, etc. of harmonic quadruples see, for example, [a1]–[a3].
References
| [a1] | M. Berger, "Geometry" , I , Springer (1987) pp. 270 |
| [a2] | H.S.M. Coxeter, "Projective geometry" , Blaisdell (1964) |
| [a3] | H.S.M. Coxeter, "The real projective plane" , McGraw-Hill (1949) |
Harmonic quadruple. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Harmonic_quadruple&oldid=17134