Hankel functions

Cylinder functions of the third kind. They may be defined in terms of Bessel functions as follows:

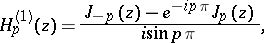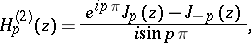where is not an integer. This implies the important relations

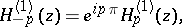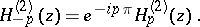Hankel functions are complex for real values of ; however,

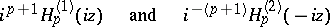are real if is real and positive. Hankel functions have simple asymptotic representations for large :

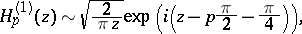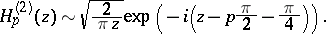The Hankel function of a "half-integral" argument 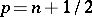can be expressed in terms of elementary functions, in particular:

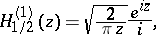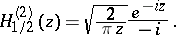These functions were introduced by H. Hankel in 1869.

References

[1]	E. Jahnke, F. Emde, F. Lösch, "Tafeln höheren Funktionen" , Teubner (1966)

Comments

See Cylinder functions for additional references.