Hammerstein equation
A non-linear integral equation of the type
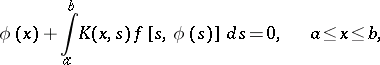 |
where  and
and  are given functions, while
are given functions, while  is the unknown function. Named after A. Hammerstein [1], who considered the case where
is the unknown function. Named after A. Hammerstein [1], who considered the case where  is a symmetric and positive Fredholm kernel, i.e. all its eigen values are positive. If, in addition, the function
is a symmetric and positive Fredholm kernel, i.e. all its eigen values are positive. If, in addition, the function  is continuous and satisfies the condition
is continuous and satisfies the condition
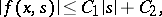 |
where  and
and  are positive constants and
are positive constants and  is smaller than the first eigen value of the kernel
is smaller than the first eigen value of the kernel 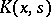 , the Hammerstein equation has at least one continuous solution. If, on the other hand,
, the Hammerstein equation has at least one continuous solution. If, on the other hand,  happens to be a non-decreasing function of
happens to be a non-decreasing function of  for any fixed
for any fixed  from the interval
from the interval  , Hammerstein's equation cannot have more than one solution. This property holds also if
, Hammerstein's equation cannot have more than one solution. This property holds also if 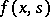 satisfies the condition
satisfies the condition
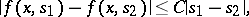 |
where the positive constant  is smaller than the first eigen value of the kernel
is smaller than the first eigen value of the kernel  . A solution of the Hammerstein equation may be constructed by the method of successive approximation (cf. Sequential approximation, method of).
. A solution of the Hammerstein equation may be constructed by the method of successive approximation (cf. Sequential approximation, method of).
References
| [1] | A. Hammerstein, "Nichtlineare Integralgleichungen nebst Anwendungen" Acta Math. , 54 (1930) pp. 117–176 |
| [2] | F.G. Tricomi, "Integral equations" , Dover, reprint (1985) |
| [3] | M.M. Vainberg, "Variational methods for the study of nonlinear operators" , Holden-Day (1964) (Translated from Russian) |
| [4] | M.A. Krasnosel'skii, "Topological methods in the theory of nonlinear integral equations" , Pergamon (1964) (Translated from Russian) |
| [5] | N.S. Smirnov, "Introduction to the theory of integral equations" , Moscow-Leningrad (1936) (In Russian) |
Hammerstein equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hammerstein_equation&oldid=13494