Hamilton operator
nabla operator,  -operator, Hamiltonian
-operator, Hamiltonian
A symbolic first-order differential operator, used for the notation of one of the principal differential operations of vector analysis. In a rectangular Cartesian coordinate system  with unit vectors
with unit vectors  , the Hamilton operator has the form
, the Hamilton operator has the form
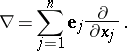 |
The application of the Hamilton operator to a scalar function 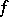 , which is understood as multiplication of the "vector"
, which is understood as multiplication of the "vector"  by the scalar
by the scalar 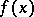 , yields the gradient of
, yields the gradient of  :
:
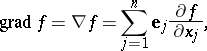 |
i.e. the vector with components 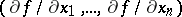 .
.
The scalar product of  with a field vector
with a field vector 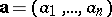 yields the divergence of
yields the divergence of  :
:
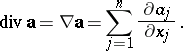 |
The vector product of  with the vectors
with the vectors 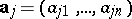 ,
, 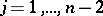 , yields the curl (rotation, abbreviated by rot) of the fields
, yields the curl (rotation, abbreviated by rot) of the fields 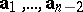 , i.e. the vector
, i.e. the vector
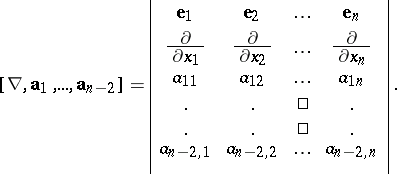 |
If 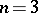 ,
,
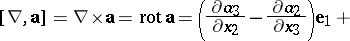 |
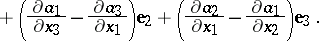 |
The scalar square of the Hamilton operator yields the Laplace operator:
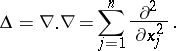 |
The following relations are valid:
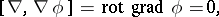 |
 |
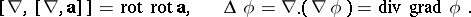 |
The Hamilton operator was introduced by W. Hamilton [1].
References
| [1] | W.R. Hamilton, "Lectures on quaternions" , Dublin (1853) |
Comments
See also Vector calculus.
References
| [a1] | D.E. Rutherford, "Vector mechanics" , Oliver & Boyd (1949) |
| [a2] | T.M. Apostol, "Calculus" , 1–2 , Blaisdell (1964) |
| [a3] | H. Holman, H. Rummler, "Alternierende Differentialformen" , B.I. Wissenschaftsverlag Mannheim (1972) |
Hamilton operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hamilton_operator&oldid=11494