Haefliger structure

of codimension and class on a topological space

A structure defined by means of a Haefliger atlas (also called a Haefliger cocycle) , where the are open subsets covering , the

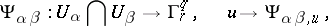are continuous mappings of into the sheaf of germs (cf. Germ) of local 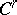-diffeomorphisms of the space 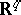, and

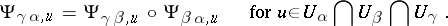Two Haefliger atlases determine one and the same Haefliger structure if they are part of some larger Haefliger atlas. (Thus, a Haefliger structure can also be defined as a maximal Haefliger atlas.) If on 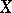a Haefliger structure 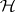is given by means of an atlas 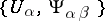and if 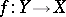is a continuous mapping, then the atlas 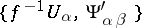, where 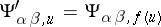, defines the induced Haefliger structure 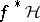(which does not depend on the concrete choice of the atlas specifying ).

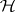Let 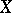be a manifold endowed with a foliation 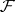by means of submersions 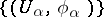that are compatible in the sense that if 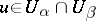, then there exists a local 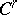-diffeomorphism 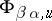by means of which one can go over from 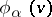to :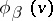

(*)

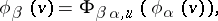for all sufficiently close to . If one puts 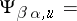germ of in , then 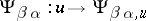is a mapping 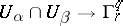, and 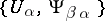is a Haefliger atlas. Here 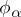can be recovered uniquely from the Haefliger atlas: 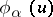is that point in which the germ is 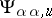. The resulting correspondence between foliations and certain Haefliger structures does not depend on the accidentals of the construction (the choice of the system 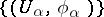); distinct foliations correspond to distinct Haefliger structures, but there exist Haefliger structures that do not correspond to any foliation. Therefore, a Haefliger structure is a generalization of the concept of a foliation.

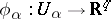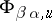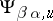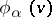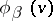In the general case one may define for a Haefliger structure, as above, a mapping . If is a representative of the germ , then and are connected in some neighbourhood of , as before, by the relation (*). But since 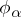and 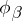are not necessarily submersions, generally speaking, one cannot determine 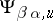uniquely from (*). Therefore, in general, one has to define a Haefliger structure not in terms of 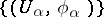, but by including in the definition.

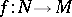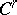If is a -mapping of manifolds that is transversal to the leaves of a foliation 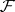of codimension 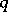and class 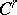, given on 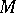, then the partition of 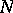into the connected components of the inverse images of the leaves of 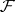is a foliation, which is naturally said to be induced; it is denoted by . If a compatible system of submersions 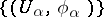specifies 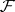, then 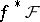is determined by the compatible system of submersions ; in this case the induced Haefliger structure is essentially the same as the induced foliation. But if 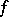is not transversal to the leaves of 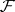, then there is no induced foliation, but only an induced Haefliger structure. Therefore, in the homotopy theory of foliations the reversion to Haefliger structures is inevitable, at least in certain intermediate stages of the argument.

It was observed (see [1], [2]) that the known connection for foliations and fibre bundles (cf. Foliation) between their classification and continuous mappings into the classifying space is preserved for Haefliger structures. This classifying space is denoted by 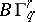for a Haefliger structure of codimension 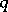and class 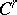. There is also a certain "universal" Haefliger structure 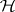in 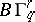(in this respect rather resembles the universal foliation (fibre bundle)). For any "good" topological space 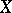(for example, a cellular polyhedron) any Haefliger structure on 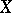is induced from by some continuous mapping 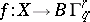. 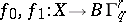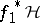Two mappings are homotopic if and only if the Haefliger structures and are concordant, that is, are obtained from the "restriction" of a certain Haefliger structure on the "cylinder" to the "bottom" and the "top" .

All that has been said refers also to topological, analytic, and piecewise-linear Haefliger structures, and the first two cases are formally subsumed under the preceding text if one takes 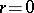or 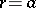, while the last one requires a certain rephrasing.

References

[1]	A. Haefliger, "Feuilletages sur les variétés ouvertes" Topology , 9 : 2 (1970) pp. 183–194
[2]	A. Haefliger, "Homotopy and integrability" N.H. Kuiper (ed.) , Manifolds (Amsterdam, 1970) , Lect. notes in math. , 197 , Springer (1971) pp. 133–163
[3]	H. Lawson, "The quantitative theory of foliations" , Amer. Math. Soc. (1977)
[4]	D.B. Fuks, "Cohomology of infinite-dimensional Lie algebras and characteristic classes of foliations" J. Soviet Math. , 11 (1979) pp. 922–980 Itogi Nauk. i Tekhn. Sovrem. Probl. Mat. , 10 (1978) pp. 179–285
[5]	D.B. Fuks, "Foliations" J. Soviet Math. , 18 (1982) pp. 255–291 Itogi Nauk. i Tekhn. Algebra Topol. Geom. , 18 (1981) pp. 151–213