Hadwiger hypothesis
Hadwiger conjecture
A problem in combinatorial geometry on the covering of a convex body by figures of a special form, which was put forth by H. Hadwiger in [1]. Let 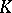 be a convex body in the
be a convex body in the  -dimensional Euclidean space
-dimensional Euclidean space 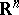 , and let
, and let 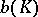 the minimal number of bodies homothetic to
the minimal number of bodies homothetic to 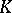 with homothety coefficient
with homothety coefficient 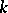 ,
, 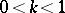 , that are sufficient to cover
, that are sufficient to cover 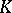 . The Hadwiger conjecture consists in the following: Any bounded set
. The Hadwiger conjecture consists in the following: Any bounded set 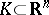 satisfies the inequality
satisfies the inequality
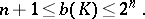 | (*) |
Here the equality  characterizes a parallelepiped (see [1]). The Hadwiger conjecture has been proved for
characterizes a parallelepiped (see [1]). The Hadwiger conjecture has been proved for 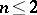 ; for
; for 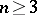 there are (1988) only partial results. For example, for any
there are (1988) only partial results. For example, for any  -dimensional bounded polyhedron
-dimensional bounded polyhedron 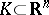 in which any two vertices belong to two distinct parallel supporting hyperplanes to
in which any two vertices belong to two distinct parallel supporting hyperplanes to 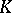 the inequality (*) holds. Here
the inequality (*) holds. Here  coincides with the number of vertices of
coincides with the number of vertices of 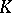 , but in the set of such polyhedra the equality
, but in the set of such polyhedra the equality 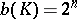 has been verified only for parallelepipeds. This result is connected with the solution of the Erdös problem on the number of points in
has been verified only for parallelepipeds. This result is connected with the solution of the Erdös problem on the number of points in 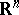 any three of which form a triangle that is not obtuse angled. The Hadwiger conjecture is also connected with covering; decomposition and the illumination problem. For example, the Hadwiger conjecture can be regarded as a generalization of the Borsuk problem on the decomposition of a set into parts of smaller diameter, when
any three of which form a triangle that is not obtuse angled. The Hadwiger conjecture is also connected with covering; decomposition and the illumination problem. For example, the Hadwiger conjecture can be regarded as a generalization of the Borsuk problem on the decomposition of a set into parts of smaller diameter, when  is replaced by a Minkowski space. For an unbounded set
is replaced by a Minkowski space. For an unbounded set 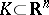 the number
the number 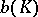 is either equal to
is either equal to 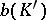 , where
, where 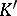 is a convex bounded body of lower dimension, or is
is a convex bounded body of lower dimension, or is 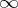 . For example, for
. For example, for 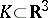 the number
the number 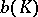 can only take one of the values
can only take one of the values 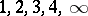 (see [2]).
(see [2]).
References
| [1] | H. Hadwiger, "Ueber Treffanzahlen bei translationsgleichen Eikörpern" Arch. Math. (Basel) , 8 (1957) pp. 212–213 |
| [2] | V.G. Boltyanskii, P.S. Soltan, "The combinatorial geometry of various classes of convex sets" , Kishinev (1978) (In Russian) |
Comments
For bounded centrally-symmetric bodies 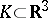 Hadwiger's conjecture holds, see [a1].
Hadwiger's conjecture holds, see [a1].
See also Geometry of numbers and the standard work [a4].
References
| [a1] | M. Lassak, "Solution of Hadwiger's covering problem for centrally symmetric convex bodies in 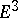 " J. London Math. Soc. (2) , 30 (1984) pp. 501–511 " J. London Math. Soc. (2) , 30 (1984) pp. 501–511 |
| [a2] | L. Danzer, B. Grünbaum, V.L. Klee, "Helly's theorem and its relatives" V.L. Klee (ed.) , Convexity , Proc. Symp. Pure Math. , 7 , Amer. Math. Soc. (1963) pp. 101–180 |
| [a3] | H. Hadwiger, H. Debrunner, "Kombinatorische Geometrie in der Ebene" L'Enseign. Math. , 2 (1959) |
| [a4] | P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) pp. Sect. (iv) (Updated reprint) |
Hadwiger hypothesis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hadwiger_hypothesis&oldid=16700