Hadamard variational formula
The formula
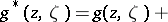 |
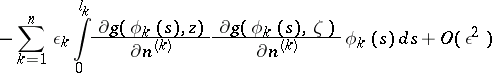 |
for the Green function 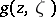 of an
of an  -connected domain
-connected domain  (
(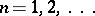 ) in the complex
) in the complex  -plane. Hadamard's variational formula is applicable if: 1) the boundary components
-plane. Hadamard's variational formula is applicable if: 1) the boundary components 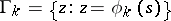 of the domain
of the domain 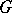 are twice-differentiable closed Jordan curves, where
are twice-differentiable closed Jordan curves, where  is the arc length on
is the arc length on 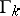 ,
, 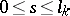 ; 2) the numbers
; 2) the numbers 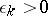 are so small that the ends of the segments of the interior normals
are so small that the ends of the segments of the interior normals 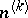 to
to 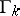 of length
of length 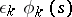 lying in
lying in 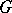 form continuously-differentiable curves, bounding an
form continuously-differentiable curves, bounding an  -connected domain
-connected domain 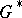 ,
, 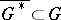 ; and 3)
; and 3) 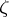 is a fixed point in
is a fixed point in 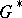 . Hadamard's variational formula represents the Green function
. Hadamard's variational formula represents the Green function 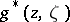 of the domain
of the domain 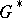 by
by 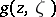 with a uniform estimate
with a uniform estimate 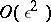 ,
, 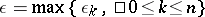 , of the remainder term in the direct product of the domain
, of the remainder term in the direct product of the domain 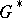 and an arbitrary compact set in
and an arbitrary compact set in 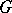 . Hadamard's variational formula can also be used for the Green function of a finite Riemann surface with boundary.
. Hadamard's variational formula can also be used for the Green function of a finite Riemann surface with boundary.
The formula was proposed by J. Hadamard [1].
References
| [1] | J. Hadamard, "Memoire sur le problème d'analyse relatif a l'équilibre des plagues élastiques eucastrées" Mém. prés. par divers savants à l'Acad. Sci. , 33 (1907) (Also: Oeuvres, Vol. II, C.N.R.S. (1968), pp. 515–631) |
| [2] | M. Schiffer, D.C. Spencer, "Functionals of finite Riemann surfaces" , Princeton Univ. Press (1954) |
Comments
For a proof of Hadamard's variational formula under minimal hypotheses, plus further references, see [a1].
References
| [a1] | S.E. Warschawski, "On Hadamard's variation formula for Green's function" J. Math. Mech. , 9 (1960) pp. 497–511 |
Hadamard variational formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hadamard_variational_formula&oldid=12275