Haar condition
A condition on continuous functions 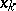 ,
, 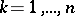 , that are linearly independent on a bounded closed set
, that are linearly independent on a bounded closed set 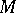 of a Euclidean space. The Haar condition, stated by A. Haar [1], ensures for any continuous function
of a Euclidean space. The Haar condition, stated by A. Haar [1], ensures for any continuous function 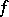 on
on 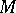 the uniqueness of the polynomial of best approximation in the system
the uniqueness of the polynomial of best approximation in the system 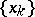 , that is, of the polynomial
, that is, of the polynomial
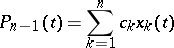 | (*) |
for which
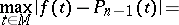 |
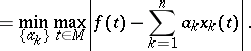 |
The Haar condition says that any non-trivial polynomial of the form (*) can have at most 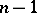 distinct zeros on
distinct zeros on 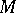 . For any continuous function
. For any continuous function 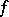 on
on 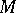 there exists a unique polynomial of best approximation in the system
there exists a unique polynomial of best approximation in the system 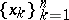 if and only if the system satisfies the Haar condition. A system of functions satisfying the Haar condition is called a Chebyshev system. For such systems the Chebyshev theorem and the de la Vallée-Poussin theorem (on alternation) hold. The Haar condition is sufficient for the uniqueness of the polynomial of best approximation in the system
if and only if the system satisfies the Haar condition. A system of functions satisfying the Haar condition is called a Chebyshev system. For such systems the Chebyshev theorem and the de la Vallée-Poussin theorem (on alternation) hold. The Haar condition is sufficient for the uniqueness of the polynomial of best approximation in the system 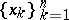 with respect to the metric of
with respect to the metric of 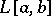 (
(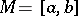 ) for any continuous function on
) for any continuous function on 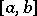 .
.
References
| [1] | A. Haar, "Die Minkowskische Geometrie and die Annäherung an stetige Funktionen" Math. Ann. , 78 (1918) pp. 249–311 |
| [2] | N.I. [N.I. Akhiezer] Achiezer, "Theory of approximation" , F. Ungar (1956) (Translated from Russian) |
Comments
References
| [a1] | E.W. Cheney, "Introduction to approximation theory" , McGraw-Hill (1966) pp. Chapt. 3 |
| [a2] | A.S.B. Holland, B.N. Sahney, "The general problem of approximation and spline functions" , R.E. Krieger (1979) pp. Chapt. 2 |
| [a3] | G.G. Lorentz, S.D. Riemenschneider, "Approximation and interpolation in the last 20 years" , Birkhoff interpolation , Addison-Wesley (1983) pp. xix-lv; in particular, xx-xxiii |
| [a4] | A.F. Timan, "Theory of approximation of functions of a real variable" , Pergamon (1963) pp. Chapt. 2 (Translated from Russian) |
| [a5] | J.R. Rice, "The approximation of functions" , 1. Linear theory , Addison-Wesley (1964) |
| [a6] | G. Meinardus, "Approximation of functions: theory and numerical methods" , Springer (1967) |
| [a7] | D.S. Bridges, "Recent developments in constructive approximation theory" A.S. Troelstra (ed.) D. van Dalen (ed.) , The L.E.J. Brouwer Centenary Symposium , Studies in logic , 110 , North-Holland (1982) pp. 41–50 |
Haar condition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Haar_condition&oldid=11643