Difference between revisions of "H-principle"
m (AUTOMATIC EDIT (latexlist): Replaced 53 formulas out of 54 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (Automatically changed introduction) |
||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 54 formulas, 53 were replaced by TEX code.--> | Out of 54 formulas, 53 were replaced by TEX code.--> | ||
Revision as of 17:41, 1 July 2020
homotopy principle
A term having its origin in papers by M. Gromov in the 1960s and 1970s, some in collaboration with Y. Eliashberg and V. Rokhlin. It applies to partial differential equations or inequalities which have, very roughly speaking, as many solutions as predicted by topology.
The foundational example is the immersion theorem of S. Smale and M. Hirsch, which states the following: Let $V$ and $W$ be smooth manifolds without boundary and suppose that 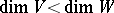 or that $V$ is non-compact. Then a smooth mapping $f : V \rightarrow W$ is homotopic (cf. also Homotopy) to a smooth immersion if and only if it can be covered by a continuous bundle mapping $\varphi : T V \rightarrow T W$ which is injective on each fibre. The $h$-principle provides a general language to formulate this and other geometric problems.
or that $V$ is non-compact. Then a smooth mapping $f : V \rightarrow W$ is homotopic (cf. also Homotopy) to a smooth immersion if and only if it can be covered by a continuous bundle mapping $\varphi : T V \rightarrow T W$ which is injective on each fibre. The $h$-principle provides a general language to formulate this and other geometric problems.
Let $\pi : X \rightarrow V$ be a smooth fibration and let $X ^ { ( r ) }$ the space of $r$-jets of smooth sections of $\pi$. A section of the bundle $X ^ { ( r ) } \rightarrow V$ is called holonomic if it is the $r$-jet $J _ { f } ^ { r }$ of a section $f$ of $\pi$. A differential relation (of order $r$) imposed on sections $f : V \rightarrow X$ is a subset $\mathcal{R} \subset X ^ { ( r ) }$. On says that $\mathcal{R}$ satisfies the $h$-principle if every section $\sigma : V \rightarrow \mathcal{R}$ is homotopic to a holonomic section $J _ { f } ^ { r }$ through a homotopy of sections $V \rightarrow \mathcal{R}$.
There are several versions of the $h$-principle (relative, with parameters, etc.). For instance, the $h$-principle is called dense if a section of $\mathcal{R}$ can be homotoped into a holonomic section by a homotopy $C ^ { 0 }$-close to the original section.
To formulate the immersion theorem above in this language, one takes the trivial fibration $X = V \times W \rightarrow V$ and defines the immersion relation $\mathcal{I} \subset X ^ { ( 1 ) }$ by stipulating that $\mathcal{I}_{ ( v , w )}$ consist of the injective linear mappings in $X _ { ( v , w ) } ^ { ( 1 ) } = \operatorname { Hom } ( T _ { v } V \rightarrow T _ { w } W )$. The immersion theorem then says that $\cal I$ satisfies the $h$-principle.
A surprising number of geometrically significant relations satisfy the $h$-principle, and Gromov has developed powerful methods for proving the $h$-principle. The fundamental reference for this subject is [a1]. The principal methods for proving the $h$-principle are removal of singularities, continuous sheaves, and convex integration.
The simplest instance of relations satisfying the $h$-principle is arguably that of open relations over open manifolds (or in the case of extra dimension), subject to some naturality conditions. A very readable account of this theory can be found in [a2]. One particular application of this form of the $h$-principle is to symplectic and contact geometry: If $V ^ { 2 n }$ is open, then every non-degenerate $2$-form $\beta$ (i.e. satisfying $\beta ^ { n } \neq 0$) is homotopic to an exact non-degenerate $2$-form, i.e. an exact symplectic form. Similarly, if $V ^ { 2 n + 1 }$ is open and $\alpha , \beta$ are a $1$-form, respectively a $2$-form, with $\alpha \wedge \beta ^ { n } \neq 0$, then $\alpha$ is homotopic to a contact form $\gamma$, that is, $\gamma \wedge ( d \gamma ) ^ { n } \neq 0$. Other important applications of the $h$-principle are the Nash–Kuiper $C ^ { 1 }$-isometric immersion theorem and the classification of isotropic immersions (see Isotropic submanifold; Contact surgery) in contact geometry.
References
| [a1] | M. Gromov, "Partial differential relations" , Ergebn. Math. Grenzgeb. (3) , 9 , Springer (1986) MR0864505 Zbl 0651.53001 |
| [a2] | A. Haefliger, "Lectures on the theorem of Gromov" , Proc. Liverpool Singularities Sympos. II , Lecture Notes Math. , 209 , Springer (1971) pp. 128–141 MR0334241 Zbl 0222.57020 |
H-principle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=H-principle&oldid=49987