Groupoid
A universal algebra with one binary operation. It is the broadest class of such algebras: groups, semi-groups, quasi-groups — all these are groupoids of a special type. An important concept in the theory of groupoids is that of isotopy of operations. On a set  let there be defined two binary operations, denoted by
let there be defined two binary operations, denoted by  and
and  ; they are isotopic if there exist three one-to-one mappings
; they are isotopic if there exist three one-to-one mappings  ,
,  and
and  of
of  onto itself such that
onto itself such that  for all
for all  . A groupoid that is isotopic to a quasi-group is itself a quasi-group; a groupoid with a unit element that is isotopic to a group, is also isomorphic to this group. For this reason, in group theory the concept of isotopy is not used: For groups isotopy and isomorphism coincide.
. A groupoid that is isotopic to a quasi-group is itself a quasi-group; a groupoid with a unit element that is isotopic to a group, is also isomorphic to this group. For this reason, in group theory the concept of isotopy is not used: For groups isotopy and isomorphism coincide.
A groupoid with cancellation is a groupoid in which either of the equations  ,
,  implies
implies  , where
, where  ,
,  and
and  are elements of the groupoid. Any groupoid with cancellation is imbeddable into a quasi-group. A homomorphic image of a quasi-group is a groupoid with division, that is, a groupoid in which the equations
are elements of the groupoid. Any groupoid with cancellation is imbeddable into a quasi-group. A homomorphic image of a quasi-group is a groupoid with division, that is, a groupoid in which the equations  and
and  are solvable (but do not necessarily have unique solutions).
are solvable (but do not necessarily have unique solutions).
A set with one partial binary operation (i.e. one not defined for all pairs of elements) is said to be a partial groupoid. Any partial subgroupoid of a free partial groupoid is free.
References
| [1] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
| [2] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
| [3] | O. Boruvka, "Foundations of the theory of groupoids and groups" , Wiley (1976) (Translated from German) |
| [4] | R.H. Bruck, "A survey of binary systems" , Springer (1958) |
Comments
There is another, conflicting, use of the term "groupoid" in mathematics, which was introduced by H. Brandt [a1]. A groupoid may conveniently be defined as a (small) category in which every morphism is an isomorphism; equivalently, it is a set  equipped with a unary operation
equipped with a unary operation 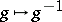 and a partial binary operation
and a partial binary operation  satisfying
satisfying
1)  and
and  are always defined;
are always defined;
2)  is defined if and only if
is defined if and only if  ;
;
3) if  and
and  are defined, then
are defined, then  and
and 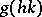 are defined and equal;
are defined and equal;
4) each of  ,
,  ,
,  , and
, and  is equal to
is equal to  if it is defined.
if it is defined.
Groupoids, as a special case of categories, play an important role in many areas of application of category theory, including algebra [a2], different geometry [a3] and topology [a4], [a5].
References
| [a1] | H. Brandt, "Ueber eine Verallgemeinerung des Gruppenbegriffes" Math. Ann. , 96 (1926) pp. 360–366 |
| [a2] | P.J. Higgins, "Categories and groupoids" , v. Nostrand-Reinhold (1971) |
| [a3] | Ch. Ehresmann, "Structures locales et catégories ordonnés" , Oeuvres complètes et commentées , Supplément aux Cahiers de Topologie et Géométrie Différentielle Catégoriques , Partie II (1980) |
| [a4] | R. Brown, "Elements of modern topology" , McGraw-Hill (1968) |
| [a5] | R. Brown, "From groups to groupoids: a brief survey" Bull. London Math. Soc. , 19 (1987) pp. 113–134 |
Groupoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Groupoid&oldid=17553