Group algebra of a locally compact group
A topological algebra with involution formed by certain functions on the group with multiplication in it defined as convolution. Let the Banach space 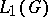 be constructed using a left-invariant Haar measure
be constructed using a left-invariant Haar measure  on a locally compact topological group
on a locally compact topological group 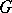 and let the multiplication in
and let the multiplication in 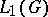 be defined as the convolution
be defined as the convolution  ; also, let the involution
; also, let the involution 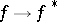 be given by the formula
be given by the formula 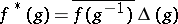 , where
, where 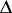 is the modular function of
is the modular function of 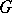 . The resulting Banach algebra with involution is said to be the group algebra of
. The resulting Banach algebra with involution is said to be the group algebra of 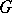 and is also denoted by
and is also denoted by 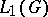 . If
. If 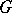 is a finite group, then the definition of the group algebra coincides with the ordinary algebraic definition of the group algebra over the field of complex numbers.
is a finite group, then the definition of the group algebra coincides with the ordinary algebraic definition of the group algebra over the field of complex numbers.
The concept of a group algebra makes it possible to use the general methods of the theory of Banach algebras in problems of group theory and, in particular, in abstract harmonic analysis. The properties of a group algebra, as a Banach algebra, reflect the properties of topological groups; thus, a group algebra contains a unit element if and only if the group is discrete; the group algebra is the direct (topological) sum of its finite-dimensional minimal two-sided ideals if and only if the group is compact. Of special importance is the concept of a group algebra in the theory of unitary representations (cf. Unitary representation) of groups: Between the continuous unitary representations of a topological group 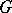 and the non-degenerate symmetric representations (cf. Involution representation) of the group algebra
and the non-degenerate symmetric representations (cf. Involution representation) of the group algebra  there exists a one-to-one correspondence. This correspondence puts a continuous unitary representation
there exists a one-to-one correspondence. This correspondence puts a continuous unitary representation 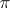 of
of 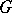 in a Hilbert space
in a Hilbert space 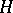 into correspondence with the representation of
into correspondence with the representation of 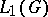 defined by
defined by
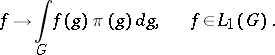 |
Group algebras of locally compact groups have a number of properties in common. In fact, any group algebra contains an approximate unit element (cf. Banach algebra), formed by the family of characteristic functions on a neighbourhood of the unit element ordered by inclusion (in decreasing order). For this reason it is possible to establish for a group algebra a correspondence between the positive functionals on the group algebra and its symmetric representations. Any group algebra is a semi-simple algebra, and has a symmetric faithful representation. In particular, the representation of a group algebra determined by the regular representation of the group is faithful. The closed left ideals of 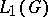 are the closed vector subspaces of
are the closed vector subspaces of 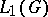 that are invariant with respect to left translation.
that are invariant with respect to left translation.
The name group algebra is also sometimes given to the Banach algebra with involution obtained from the group algebra 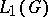 by the adjunction of a unit. There exist several other algebras with involutions, which are sometimes referred to as group algebras. These include, in particular: the algebra of measures
by the adjunction of a unit. There exist several other algebras with involutions, which are sometimes referred to as group algebras. These include, in particular: the algebra of measures 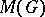 with respect to convolution, algebras with respect to ordinary multiplication, such as the algebra
with respect to convolution, algebras with respect to ordinary multiplication, such as the algebra 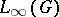 of essentially-bounded functions that are measurable by the Haar measure, and the algebra
of essentially-bounded functions that are measurable by the Haar measure, and the algebra 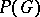 spanned by the set of complex positive-definite functions. The set
spanned by the set of complex positive-definite functions. The set 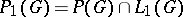 and the set
and the set 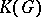 of continuous functions with compact support form algebras both with respect to convolution and with respect to ordinary multiplication. One obtains the following table, in which arrows denote inclusions:
of continuous functions with compact support form algebras both with respect to convolution and with respect to ordinary multiplication. One obtains the following table, in which arrows denote inclusions:
 |
References
| [1] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) |
| [2] | A. Guichardet, "Analyse harmonique commutative" , Dunod (1968) |
Comments
The set of all complex continuous positive-definite functions on 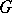 is not an algebra since 1 is in it but
is not an algebra since 1 is in it but 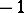 is not. However, the set of all complex linear combinations of its members, which is usually denoted
is not. However, the set of all complex linear combinations of its members, which is usually denoted 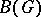 , is an algebra under the usual pointwise multiplication (see [a1], (32.10)). For all non-discrete locally compact Abelian groups
, is an algebra under the usual pointwise multiplication (see [a1], (32.10)). For all non-discrete locally compact Abelian groups 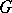 there exist continuous compactly-supported functions on
there exist continuous compactly-supported functions on 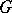 that are not in
that are not in 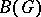 (see [a1], (33.3) and (41.19)). Thus
(see [a1], (33.3) and (41.19)). Thus 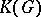 is not a subset of
is not a subset of 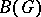 .
.
For the notion of the modular function 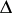 of
of 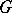 , cf. Haar measure. A symmetric representation
, cf. Haar measure. A symmetric representation  of an algebra with involution in a Hilbert space over
of an algebra with involution in a Hilbert space over 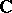 is one which satisfies
is one which satisfies 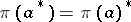 for all
for all 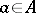 . Here the
. Here the  on the right denotes taking adjoints and the
on the right denotes taking adjoints and the  on the left refers to the involution on
on the left refers to the involution on 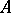 .
.
References
| [a1] | E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , 1–2 , Springer (1979) |
| [a2] | J. Dixmier, "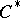 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
Group algebra of a locally compact group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Group_algebra_of_a_locally_compact_group&oldid=16083