Grothendieck group

of an additive category

An Abelian group that is assigned to an additive category by a universal additive mapping property. More exactly, let be a small additive category and let be an Abelian group. A mapping is said to be additive if for any exact sequence of objects from the relation is valid. There exists a group , called the Grothendieck group of , and an additive mapping , known as the universal mapping, such that for any additive mapping there exists a unique homomorphism 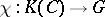that satisfies the condition .

This construction was first studied by A. Grothendieck for the categories of coherent and locally free sheaves on schemes in proving the Riemann–Roch theorem. See 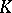-functor in algebraic geometry. The group is uniquely defined (up to isomorphism) and can be given by generators — to each object 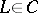there corresponds a generator — and by the relations for each exact sequence

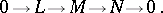If is a topological space, then the Grothendieck group of the additive category of vector bundles over is an invariant of the space, studied in (topological) 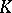-theory. If 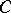is the category of non-degenerate symmetric bilinear forms on linear spaces over a field 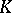, then is the Witt–Grothendieck group over (cf. Witt ring).

References

[1]	R. Swan, "The Grothendieck ring of a finite group" Topology , 2 (1963) pp. 85–110
[2]	A. Borel, J.P. Serre, "Le théorème de Riemann–Roch" Bull. Soc. Math. France , 86 (1958) pp. 97–136
[3]	M.F. Atiyah, "-theory: lectures" , Benjamin (1967)
[4]	H. Bass, "Lectures on topics in algebraic -theory" , Tata Inst. (1966)
[5]	S. Lang, "Algebra" , Addison-Wesley (1974)

Comments

One also associates a Grothendieck group 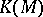to any commutative monoid as the solution of the universal problem posed by additive mappings of 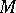into Abelian groups. It is the Abelian group with generators 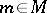and relations 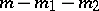, for all 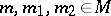such that 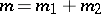in 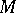. Taking, for instance, the monoid of isomorphism classes of vector bundles over a topological space (with the monoid addition induced by the direct sum) one again obtains the topological 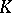-group .

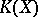When considering an additive category 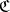in which not every short exact sequence splits, there are two possible natural associated Grothendieck groups. Both are Abelian groups generated by the isomorphism classes of objects of 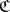. For the first there is a relation 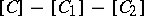whenever 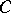is isomorphic to , and for the second there is a relation 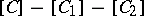whenever there is a short exact sequence 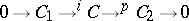. (Such a short exact sequence splits if there is a morphism 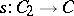such that .) Both notions occur in the literature.

The Grothendieck group 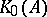defined by the additive category of finitely-generated projective modules over 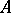(in which every short exact sequence splits of course) is sometimes called the Grothendieck group of the ring 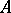. Cf. also Algebraic 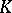-theory. Another important example of a Grothendieck group is the Picard group 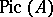of a ring (or of a scheme). It is the Grothendieck group associated to the commutative monoid of isomorphism classes of rank 1 projective modules over with the addition induced by the tensor prodect over .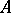

References

[a1]	H. Bass, "Algebraic -theory" , Benjamin (1968)
[a2]	M. Karoubi, "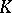-theory" , Springer (1978)
[a3]	J. Berrick, "An approach to algebraic 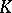-theory" , Pitman (1982)