Difference between revisions of "Grothendieck group"
Ulf Rehmann (talk | contribs) m ('exact' back replaced by 'additive') |
|||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | {{MSC|18|55N15}} | |
| + | {{TEX|done}} | ||
| − | + | The ''Grothendieck group of an additive category'' | |
| + | is an Abelian group that is assigned to an additive category by a universal additive mapping property. More exactly, let $C$ be a small [[Additive category|additive category]] with set of objects $\mathrm{Ob}(C)$ and let $G$ be an Abelian group. A mapping $\phi: \mathrm{Ob}(C) \to G$ is said to be additive if for any exact sequence $0 \to L \to M \to N \to 0$ in $C$, the relation $\phi(M)=\phi(L)+\phi(N)$ is valid. There exists a group $K(C)$, called the Grothendieck group of $C$, and an additive mapping $k:\mathrm{Ob}(C)\to K(C)$, known as the universal mapping, such that for any additive mapping $\mathrm{Ob}(C) \to G$, there exists a unique homomorphism $\xi: K(C) \to G$ that satisfies the condition $\phi=\xi \circ k$. | ||
This construction was first studied by A. Grothendieck for the categories of coherent and locally free sheaves on schemes in proving the Riemann–Roch theorem. See [[K-functor|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g045/g045170/g04517013.png" />-functor]] in algebraic geometry. The group $K(C)$ is uniquely defined (up to isomorphism) and can be given by generators — to each object $L \in C$, there corresponds a generator $[L]$ — and by the relations $[L]-[N]-[M]=0$ for each exact sequence $0 \to L \to M \to N \to 0$. | This construction was first studied by A. Grothendieck for the categories of coherent and locally free sheaves on schemes in proving the Riemann–Roch theorem. See [[K-functor|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g045/g045170/g04517013.png" />-functor]] in algebraic geometry. The group $K(C)$ is uniquely defined (up to isomorphism) and can be given by generators — to each object $L \in C$, there corresponds a generator $[L]$ — and by the relations $[L]-[N]-[M]=0$ for each exact sequence $0 \to L \to M \to N \to 0$. | ||
| Line 7: | Line 9: | ||
If $X$ is a topological space, then the Grothendieck group of the additive category of vector bundles over $X$ is an invariant of the space, studied in (topological) [[K-theory|K-theory]]. If $C$ is the category of non-degenerate symmetric bilinear forms on linear spaces over a field $k$, then $K(C)$ is the Witt–Grothendieck group of $k$ (cf. [[Witt ring|Witt ring]]). | If $X$ is a topological space, then the Grothendieck group of the additive category of vector bundles over $X$ is an invariant of the space, studied in (topological) [[K-theory|K-theory]]. If $C$ is the category of non-degenerate symmetric bilinear forms on linear spaces over a field $k$, then $K(C)$ is the Witt–Grothendieck group of $k$ (cf. [[Witt ring|Witt ring]]). | ||
| − | ==== | + | ====Comments==== |
| − | + | One also associates a Grothendieck group $K(M)$ to any commutative monoid as the solution of the universal problem posed by additive mappings of $M$ into Abelian groups. It is the Abelian group with generators $m \in M$ and relations $m-m_1-m_2$, for all $m,m_1,m_2 \in M$ such that $m=m_1+m_2$ in $M$. Taking, for instance, the monoid of isomorphism classes of vector bundles over a topological space $X$ (with the monoid addition induced by the direct sum) one again obtains the topological K-group $K(X)$. | |
| + | When considering an additive category $C$ in which not every short exact sequence splits, there are two possible natural associated Grothendieck groups. Both are Abelian groups generated by the isomorphism classes of objects of $C$. For the first there is a relation $[M]-[M_1]-[M_2]$ whenever $M$ is isomorphic to $M_1 \oplus M_2$, and for the second there is a relation $[M]-[M_1]-[M_2]$ whenever there is a short exact sequence $0 \to M_1 \to M \to M_2 \to 0$. Both notions occur in the literature. | ||
| + | The Grothendieck group $K_0(A)$ defined by the additive category of finitely-generated projective modules over a ring $A$ (in which every short exact sequence splits of course) is sometimes called the Grothendieck group of the ring $A$. Cf. also [[Algebraic K-theory|Algebraic K-theory]]. Another important example of a Grothendieck group is the [[Picard group|Picard group]] $\mathrm{Pic}(A)$ of a ring (or of a scheme). It is the Grothendieck group associated to the commutative monoid of isomorphism classes of rank 1 projective modules over $A$ with the addition induced by the tensor product over $A$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |- | ||
| + | |valign="top"|{{Ref|At}}||valign="top"| M.F. Atiyah, "K-theory: lectures", Benjamin (1967) {{MR|224083}} {{ZBL|0159.53302}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Ba}}||valign="top"| H. Bass, "Lectures on topics in algebraic K-theory", Tata Inst. (1966) {{MR|0279159}} {{ZBL|0226.13006}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Ba2}}||valign="top"| H. Bass, "Algebraic K-theory", Benjamin (1968) {{MR|249491}} {{ZBL|0174.30302}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Be}}||valign="top"| J. Berrick, "K-theory"-theory", Pitman (1982) {{MR|649409}} {{ZBL|0382.55002}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|BoSe}}||valign="top"| A. Borel, J.P. Serre, "Le théorème de Riemann–Roch" ''Bull. Soc. Math. France'', '''86''' (1958) pp. 97–136 {{MR|116022}} {{ZBL|0091.33004}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Ka}}||valign="top"| M. Karoubi, "K-theory", Springer (1978) {{MR|0488029}} {{ZBL|0382.55002}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|La}}||valign="top"| S. Lang, "Algebra", Addison-Wesley (1974) {{MR|0783636}} {{ZBL|0712.00001}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Sw}}||valign="top"| R. Swan, "The Grothendieck ring of a finite group" ''Topology'', '''2''' (1963) pp. 85–110 {{MR|0153722}} {{ZBL|0119.02905}} | ||
| + | |- | ||
| + | |} | ||
Revision as of 21:02, 16 April 2012
2020 Mathematics Subject Classification: Primary: 18-XX Secondary: 55N15 [MSN][ZBL]
The Grothendieck group of an additive category is an Abelian group that is assigned to an additive category by a universal additive mapping property. More exactly, let $C$ be a small additive category with set of objects $\mathrm{Ob}(C)$ and let $G$ be an Abelian group. A mapping $\phi: \mathrm{Ob}(C) \to G$ is said to be additive if for any exact sequence $0 \to L \to M \to N \to 0$ in $C$, the relation $\phi(M)=\phi(L)+\phi(N)$ is valid. There exists a group $K(C)$, called the Grothendieck group of $C$, and an additive mapping $k:\mathrm{Ob}(C)\to K(C)$, known as the universal mapping, such that for any additive mapping $\mathrm{Ob}(C) \to G$, there exists a unique homomorphism $\xi: K(C) \to G$ that satisfies the condition $\phi=\xi \circ k$.
This construction was first studied by A. Grothendieck for the categories of coherent and locally free sheaves on schemes in proving the Riemann–Roch theorem. See 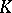 -functor in algebraic geometry. The group $K(C)$ is uniquely defined (up to isomorphism) and can be given by generators — to each object $L \in C$, there corresponds a generator $[L]$ — and by the relations $[L]-[N]-[M]=0$ for each exact sequence $0 \to L \to M \to N \to 0$.
-functor in algebraic geometry. The group $K(C)$ is uniquely defined (up to isomorphism) and can be given by generators — to each object $L \in C$, there corresponds a generator $[L]$ — and by the relations $[L]-[N]-[M]=0$ for each exact sequence $0 \to L \to M \to N \to 0$.
If $X$ is a topological space, then the Grothendieck group of the additive category of vector bundles over $X$ is an invariant of the space, studied in (topological) K-theory. If $C$ is the category of non-degenerate symmetric bilinear forms on linear spaces over a field $k$, then $K(C)$ is the Witt–Grothendieck group of $k$ (cf. Witt ring).
Comments
One also associates a Grothendieck group $K(M)$ to any commutative monoid as the solution of the universal problem posed by additive mappings of $M$ into Abelian groups. It is the Abelian group with generators $m \in M$ and relations $m-m_1-m_2$, for all $m,m_1,m_2 \in M$ such that $m=m_1+m_2$ in $M$. Taking, for instance, the monoid of isomorphism classes of vector bundles over a topological space $X$ (with the monoid addition induced by the direct sum) one again obtains the topological K-group $K(X)$.
When considering an additive category $C$ in which not every short exact sequence splits, there are two possible natural associated Grothendieck groups. Both are Abelian groups generated by the isomorphism classes of objects of $C$. For the first there is a relation $[M]-[M_1]-[M_2]$ whenever $M$ is isomorphic to $M_1 \oplus M_2$, and for the second there is a relation $[M]-[M_1]-[M_2]$ whenever there is a short exact sequence $0 \to M_1 \to M \to M_2 \to 0$. Both notions occur in the literature.
The Grothendieck group $K_0(A)$ defined by the additive category of finitely-generated projective modules over a ring $A$ (in which every short exact sequence splits of course) is sometimes called the Grothendieck group of the ring $A$. Cf. also Algebraic K-theory. Another important example of a Grothendieck group is the Picard group $\mathrm{Pic}(A)$ of a ring (or of a scheme). It is the Grothendieck group associated to the commutative monoid of isomorphism classes of rank 1 projective modules over $A$ with the addition induced by the tensor product over $A$.
References
| [At] | M.F. Atiyah, "K-theory: lectures", Benjamin (1967) MR224083 Zbl 0159.53302 |
| [Ba] | H. Bass, "Lectures on topics in algebraic K-theory", Tata Inst. (1966) MR0279159 Zbl 0226.13006 |
| [Ba2] | H. Bass, "Algebraic K-theory", Benjamin (1968) MR249491 Zbl 0174.30302 |
| [Be] | J. Berrick, "K-theory"-theory", Pitman (1982) MR649409 Zbl 0382.55002 |
| [BoSe] | A. Borel, J.P. Serre, "Le théorème de Riemann–Roch" Bull. Soc. Math. France, 86 (1958) pp. 97–136 MR116022 Zbl 0091.33004 |
| [Ka] | M. Karoubi, "K-theory", Springer (1978) MR0488029 Zbl 0382.55002 |
| [La] | S. Lang, "Algebra", Addison-Wesley (1974) MR0783636 Zbl 0712.00001 |
| [Sw] | R. Swan, "The Grothendieck ring of a finite group" Topology, 2 (1963) pp. 85–110 MR0153722 Zbl 0119.02905 |
Grothendieck group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Grothendieck_group&oldid=24624