Grothendieck category
An Abelian category with a set of generators (cf. Generator of a category) and satisfying the following axiom: There exist coproducts (sums) of arbitrary families of objects, and for each directed family of subobjects  ,
,  , of an object
, of an object  , and any subobject
, and any subobject  , the following equality is valid:
, the following equality is valid:
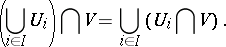 |
The category of left (right)  -modules over an arbitrary associative ring
-modules over an arbitrary associative ring  with an identity element and the category of sheaves of
with an identity element and the category of sheaves of  -modules over an arbitrary topological space are Grothendieck categories. A full subcategory
-modules over an arbitrary topological space are Grothendieck categories. A full subcategory  of the category
of the category  of left
of left 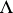 -modules is known as a localizing subcategory if it is closed with respect to colimits and if, in an exact sequence
-modules is known as a localizing subcategory if it is closed with respect to colimits and if, in an exact sequence
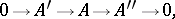 |
the object  belongs to
belongs to 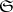 if and only if both
if and only if both 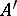 and
and 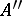 belong to
belong to  . Each localizing subcategory makes it possible to construct the quotient category
. Each localizing subcategory makes it possible to construct the quotient category  . An Abelian category is a Grothendieck category if and only if it is equivalent to some quotient category of the type
. An Abelian category is a Grothendieck category if and only if it is equivalent to some quotient category of the type 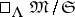 .
.
In a Grothendieck category each object has an injective envelope, and for this reason Grothendieck categories are well suited for use in homological applications.
References
| [1] | A. Grothendieck, "Sur quelques points d'algèbre homologique" Tôhoku Math. J. (2) , 9 (1957) pp. 119–221 |
| [2] | I. Bucur, A. Deleanu, "Introduction to the theory of categories and functors" , Wiley (1968) |
| [3] | N. [N. Popescu] Popesco, P. Gabriel, "Charactérisation des catégories abéliennes avec générateurs et limites inductives exactes" C.R. Acad. Sci. , 258 (1964) pp. 4188–4190 |
Comments
References
| [a1] | N. Popescu, "Abelian categories with applications to rings and modules" , Acad. Press (1973) |
Grothendieck category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Grothendieck_category&oldid=14714