Gravitation
gravity
The universal property of mutual attraction between all physical bodies. The study of gravitation was laid at the foundations of Newtonian classical mechanics. Thus, G. Galilei, who studied the quasi-homogeneous gravity field at the Earth's surface, formulated the law of inertia and found that a force acting upon a body can be measured by acceleration; J. Kepler and I. Newton studied the gravitational effect of a point with a large mass on a second point whose mass is much smaller. Kepler's studies led Newton to the discovery of the law of universal gravitation:
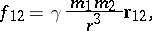 | (1) |
where 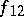 is the force of gravitation acting on the point with mass
is the force of gravitation acting on the point with mass 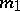 ,
, 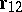 is the radius vector drawn from this point to the point with mass
is the radius vector drawn from this point to the point with mass 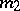 ,
,  is the distance between the points,
is the distance between the points, 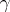 is the gravitational constant
is the gravitational constant 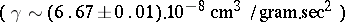 ; also,
; also, 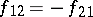 . Thus, the absolute value
. Thus, the absolute value 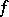 of the gravitational force vector is equal to
of the gravitational force vector is equal to  .
.
On passing from point masses to volumes, Newton's law of gravitation leads to the theory of the Newton potential, which describes the phenomenon of gravitation in terms of classical non-relativistic physics. The fundamentals of this theory are described by formula (1), represented in the form
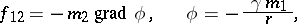 |
where 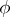 is the potential of the gravity field produced by the point of mass
is the potential of the gravity field produced by the point of mass 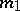 , so that
, so that 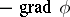 may be regarded as the field strength of the gravity field. Hence it follows, if certain conditions are satisfied, that masses distributed with density
may be regarded as the field strength of the gravity field. Hence it follows, if certain conditions are satisfied, that masses distributed with density 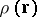 generate a field, which is determined by the Poisson equation
generate a field, which is determined by the Poisson equation
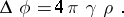 |
Outside masses which are centrally-symmetric distributed, the potential coincides with the potential of a material point located at the centre whose mass is equal to the sum of all masses (Newton's theorem). The field equation of the Newton potential, which describes gravitation, supposes the principle of action at a distance — the propagation of the gravitational effects at an infinite velocity — as well as the existence of an absolute space and an absolute time; this, however, is only a good approximation to reality. Celestial mechanics, a number of problems in astrophysics, gravimetry, aeronautics, and cosmonautics are based on the theory of the Newton potential.
A body in a given gravitational field has acceleration
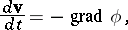 |
i.e. all bodies in a given gravitational field move at the same acceleration.
The Poisson equation of the classical theory of gravitation does not explain the internal structural mechanism of gravitation. There are many non-relativistic hypotheses on the nature of gravitation. The first attempts at explaining the reason why bodies fall to the ground date as far back as Antiquity (Plato, Aristoteles); they were continued by Leonardo da Vinci, N. Copernicus, G. Roberval, and R. Hooke. The following workers studied the nature of gravitation subsequent to Newton's times: I. Kant (the theory of two material forces — attraction and repulsion), R. Bošcović (who tried to reduce all interactive forces to a single universal force), M.V. Lomonosov, and G.L. Lesage (who assumed the existence of a special "gravitational matter" ). The hypotheses which were advanced as to the nature of gravitation included the "ether-shock" , "kinetic" , "wave" , "shock" , "hydrodynamic" , etc. hypotheses [8]. All these theories are now of mere historical interest, and the modern solution of the problem involves the construction of a quantum field theory — a problem posed to modern physics, but not yet solved.
Newton's theory of gravitation, while being in very good agreement with the experimental results, has the following drawbacks: the field of the Newton potential does not conform to the principle of action at small distances, that is, to the fact that the rate of propagation of gravitational disturbances is finite; it is not Lorentz-invariant (cf. Lorentz transformation) as is the case, for example, for the electromagnetic field; there exist at least two astronomical effects for which it fails to provide a quantitative explanation (the shift in the perihelion of Mercury and the deviation of light rays in the vicinity of the Sun). These and certain other considerations led to the genesis of Einstein's gravitational theory, a general relativistic theory which was historically a deduction from the equivalence principle (the impossibility of differentiation between the gravity field and a non-inertial coordinate system) and the principle of general covariance (the geometry of space is invariant under the group of continuously-differentiable non-degenerate transformations of coordinate systems). Modern work indicates, however, that a more complicated system of axioms is required for the construction of such a theory.
General relativity theory is the leading modern gravitational theory. Mathematically this theory is based on the following assumptions: the geometry of the physical space-time is four-dimensional. It is the Riemannian geometry of the space 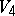 with the metric signature
with the metric signature  . There are no gravitational forces (as
. There are no gravitational forces (as  -vectors), while the equations of motion of experimental objects in the gravitational field are determined by the geodesic lines in
-vectors), while the equations of motion of experimental objects in the gravitational field are determined by the geodesic lines in 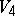 . For experimental bodies with a non-zero rest mass these geodesics are non-isotropic curves, while for particles of photon type they are isotropic. The equations of motion are the four-dimensional covariant analogues of Newton's law of inertia, while there is no covariant analogue of Newton's second law for gravitational forces. The part of the "potential" of the gravitational field is played by the components of the metric tensor
. For experimental bodies with a non-zero rest mass these geodesics are non-isotropic curves, while for particles of photon type they are isotropic. The equations of motion are the four-dimensional covariant analogues of Newton's law of inertia, while there is no covariant analogue of Newton's second law for gravitational forces. The part of the "potential" of the gravitational field is played by the components of the metric tensor 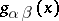 , for which the equations of the gravity field are postulated:
, for which the equations of the gravity field are postulated:
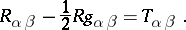 |
Here 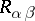 are the components of the contracted Riemann tensor,
are the components of the contracted Riemann tensor, 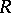 is its linear invariant and
is its linear invariant and 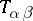 are the components of the energy-momentum tensor. In general relativity theory, as distinct from all other physical theories, the equations of motion of experimental bodies are deduced from the field equation.
are the components of the energy-momentum tensor. In general relativity theory, as distinct from all other physical theories, the equations of motion of experimental bodies are deduced from the field equation.
General relativity theory very accurately predicts the effect of the shift of the perihelion of Mercury, the effect of the deviation of light rays in the vicinity of the Sun, and also the effect of the cosmological red shift. As new experimental data became available, various physical problems could be effectively tackled. In particular, the problem of gravitational waves [13], [14] could be largely clarified; attempts at the construction of a quantum gravitational theory are in progress; various astronomical objects can be described in terms of general relativity theory.
Other modern gravitational theories have also been presented nowadays. They are based on a more general formalism (spaces of affine connections, etc.). There is also a relativistic gravitational theory in a flat space, analogous to classical electrodynamics.
References
| [1] | L.N. Sretenskii, "Theory of the Newton potential" , Moscow-Leningrad (1946) (In Russian) |
| [2] | G.N. Duboshin, "The theory of attraction" , Moscow (1961) (In Russian) |
| [3] | A. Einstein, , Selected works , 1–2 , Moscow (1966) (In Russian) |
| [4] | V.A. [V.A. Fok] Fock, "The theory of space, time and gravitation" , Macmillan (1954) (Translated from Russian) |
| [5] | J. Weber, "General relativity and gravitational waves" , Interscience (1961) |
| [6] | J.L. Synge, "Relativity: the general theory" , North-Holland & Interscience (1960) pp. Chapt. II |
| [7] | A.Z. Petrov, "New methods in general relativity theory" , Moscow (1966) (In Russian) |
| [8] | I.I. Karal'nikova, "The history of the development of the pre-relativistic interpretations on the nature of gravitation" Uchen. Zap. Yaroslavsk. Ped. Inst. Kafedra Astron. i Teoret. Fiz. , 56 (1963) (In Russian) |
| [9] | Ya.B. Zel'dovich, I.D. Novikov, "Relativistic astrophysics" , 1 - Stars and relativity; 2 - Structure and evolution of the Universe , Chicago (1971–1983) (Translated from Russian) |
| [10] | A.Z. Petrov, "The general theory of relativity" , The development of physics in the USSR , 1 , Moscow (1967) (In Russian) |
| [11] | Ya.B. Zel'dovich, I.D. Novikov, "Relativistic astrophysics" , 1. Stars and relativity , Chicago (1971) (Translated from Russian) |
| [12] | Ya.B. Zel'dovich, I.D. Novikov, "Relativistic astrophysics" , 2. Structure and evolution of the universe , Chicago (1983) (Translated from Russian) |
| [13] | R.A. Isaacson, Phys. Rev. , 166 (1968) pp. 1263 |
| [14] | R.A. Isaacson, Phys. Rev. , 166 (1968) pp. 1272 |
Comments
References
| [a1] | W.D. McMillan, "The theory of the potential" , McGraw-Hill (1930) |
| [a2] | M. Jammer, "Concepts of force" , Harvard Univ. Press (1957) (Especially Chapt. 10) |
| [a3] | I.B. Cohen, "The "principia" , universal gravitation, and the "Newtonian style" in relation to the Newtonian revolution in science" Z. Bechler (ed.) , Contemporary Newtonian research , Reidel (1982) pp. 21–108 |
| [a4] | R.S. Westfall, "Force in Newtonian physics" , Macdonald (1971) |
| [a5] | R.A. Hulse, J.H. Taylor, Astrophysics J. Lett. , 195 (1975) pp. L51 |
| [a6] | S.L. Shapiro, S.A. Teukolsky, "Black holes, white dwarfs and neutron stars" , Wiley (1983) pp. 479 |
| [a7] | C.M. DeWitt (ed.) B.S. DeWitt (ed.) , Relativity, groups and topology , Gordon & Breach (1964) |
| [a8] | H. Weyl, "Space-time-matter" , Dover, reprint (1950) (Translated from German) |
Gravitation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gravitation&oldid=18231