Grassmann manifold
Grassmannian
The set  ,
,  , of all
, of all  -dimensional subspaces in an
-dimensional subspaces in an  -dimensional vector space
-dimensional vector space  over a skew-field
over a skew-field  . If
. If  is a field, then
is a field, then  can be imbedded in a
can be imbedded in a  -dimensional projective space over
-dimensional projective space over 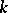 as a compact algebraic variety with the aid of Grassmann coordinates (cf. Exterior algebra). In the study of the geometrical properties of a Grassmann manifold an important role is played by the so-called Schubert varieties
as a compact algebraic variety with the aid of Grassmann coordinates (cf. Exterior algebra). In the study of the geometrical properties of a Grassmann manifold an important role is played by the so-called Schubert varieties 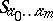 ,
, 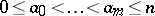 , which are defined as follows. If
, which are defined as follows. If  is a flag of subspaces, i.e. a chain of subspaces such that also
is a flag of subspaces, i.e. a chain of subspaces such that also 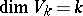 , then
, then
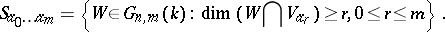 |
Any 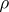 -dimensional algebraic subvariety in a Grassmann manifold
-dimensional algebraic subvariety in a Grassmann manifold 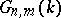 is equivalent to a unique integer combination of the varieties
is equivalent to a unique integer combination of the varieties 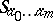 , where
, where  (see [1]).
(see [1]).
If 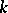 is the field
is the field 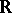 of real numbers, the field
of real numbers, the field 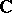 of complex numbers or the skew-field
of complex numbers or the skew-field  of quaternions, a Grassmann manifold over
of quaternions, a Grassmann manifold over 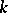 can be regarded as a compact analytic manifold (which is real if
can be regarded as a compact analytic manifold (which is real if 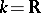 or
or  and complex if
and complex if 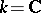 ). These manifolds are distinguished by the fact that they are the classifying spaces for the classical groups (cf. Classical group)
). These manifolds are distinguished by the fact that they are the classifying spaces for the classical groups (cf. Classical group) 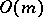 ,
, 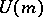 and
and 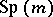 , respectively. More exactly, for any CW-complex
, respectively. More exactly, for any CW-complex 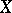 of dimension
of dimension 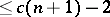 , where
, where  1, 2 and 4, respectively, the set of isomorphism classes of
1, 2 and 4, respectively, the set of isomorphism classes of 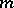 -dimensional vector bundles over
-dimensional vector bundles over 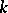 with base
with base 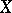 is in a natural one-to-one correspondence with the set of homotopy classes of continuous mappings
is in a natural one-to-one correspondence with the set of homotopy classes of continuous mappings 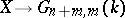 [2]. A similar theory concerning the groups
[2]. A similar theory concerning the groups 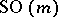 and
and 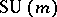 leads to the study of the Grassmann manifold
leads to the study of the Grassmann manifold 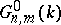 (
(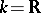 or
or 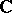 ) of oriented
) of oriented 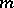 -dimensional spaces in
-dimensional spaces in  . The manifolds listed above are closely connected, in particular, with the theory of characteristic classes (cf. Characteristic class).
. The manifolds listed above are closely connected, in particular, with the theory of characteristic classes (cf. Characteristic class).
The role played by Grassmann manifolds in topology necessitated a detailed study of their topological invariants. The oldest method of this study was based on Schubert varieties, with the aid of which a cell decomposition for 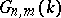 (
(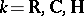 ) is readily constructed. It is found, in particular, that the cycles
) is readily constructed. It is found, in particular, that the cycles 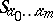 form a basis of the homology groups
form a basis of the homology groups 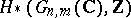 ,
, 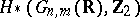 ,
,  . Cohomology algebras of Grassmann manifolds and the effect of Steenrod powers on them have also been thoroughly studied .
. Cohomology algebras of Grassmann manifolds and the effect of Steenrod powers on them have also been thoroughly studied .
Another aspect of the theory of Grassmann manifolds is that they are homogeneous spaces of linear groups over the corresponding skew-field, and represent basic examples of irreducible symmetric spaces (cf. Symmetric space).
Manifolds which are analogous to Grassmann manifolds can also be constructed from subspaces of infinite-dimensional vector spaces. In particular, an important role in the theory of deformation of analytic structures is played by a Banach analytic manifold 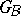 , the elements of which are the closed subspaces of a Banach space
, the elements of which are the closed subspaces of a Banach space  over
over 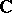 with a closed direct complement.
with a closed direct complement.
References
| [1] | W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , 2 , Cambridge Univ. Press (1952) |
| [2] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) |
| [3a] | A. Borel, "Sur la cohomogie des espaces fibrés principaux et des espaces homogènes de groupes de Lie compacts" Ann of Math. , 57 (1953) pp. 115–207 |
| [3b] | A. Borel, "La cohomologie mod 2 de certains espaces homogènes" Comm. Math. Helv. , 27 (1953) pp. 165–197 |
| [3c] | A. Borel, J.-P. Serre, "Groupes de Lie et puissances réduites de Steenrod" Amer. J. Math. , 75 (1953) pp. 409–448 |
| [4] | S.S. Chern, "Complex manifolds without potential theory" , Springer (1979) |
Comments
Choose a basis in  . For each
. For each 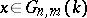 choose
choose 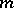 vectors generating
vectors generating  . These vectors generate an
. These vectors generate an  matrix
matrix 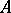 . Now assign to
. Now assign to  the point in the projective space
the point in the projective space 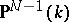 ,
,  , whose homogeneous coordinates are the determinants of all
, whose homogeneous coordinates are the determinants of all  submatrices of
submatrices of 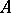 . This point does not depend on the choices made. This defines an imbedding
. This point does not depend on the choices made. This defines an imbedding 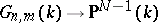 , called the Plücker imbedding. Correspondingly, these coordinates are called Plücker coordinates; they are also called Grassmann coordinates (cf. Exterior algebra and above). As a subvariety of
, called the Plücker imbedding. Correspondingly, these coordinates are called Plücker coordinates; they are also called Grassmann coordinates (cf. Exterior algebra and above). As a subvariety of 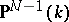 the Grassmann manifold
the Grassmann manifold 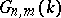 is given by a number of quadratic relations, called the Plücker relations, cf. [a1], Sect. 1.5.
is given by a number of quadratic relations, called the Plücker relations, cf. [a1], Sect. 1.5.
There are a number of different notations in use; thus, the Grassmann manifold of 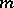 -planes in
-planes in 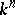 is variously denoted
is variously denoted 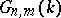 (as here),
(as here), 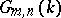 ,
,  , and
, and 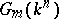 , the last one generalizing to
, the last one generalizing to 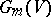 with
with 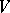 a vector space.
a vector space.
In the setting of algebraic geometry one defines the projective scheme 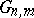 defined over
defined over 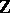 whose
whose  -points form
-points form 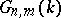 .
.
References
| [a1] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , 1–2 , Wiley (Interscience) (1978) |
| [a2] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) |
Grassmann manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Grassmann_manifold&oldid=11701