Graph automorphism

An isomorphic mapping of a graph onto itself (cf. Graph isomorphism). The set of all automorphisms of a given graph forms a group with respect to the operation of composition of automorphisms. The automorphisms of a graph 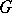generate a group 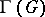of permutations of vertices, which is called the group (or vertex group) of 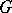, and a group of edge permutations 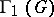, called the edge group of 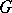. The edge group and vertex group of a graph 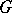without loops and multiple edges are isomorphic if and only if 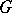contains not more than one isolated vertex and if none of its connected components is an isolated edge. For each finite group 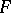there exists a graph whose automorphism group is isomorphic to 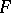. There also exist permutation groups on a set of elements which are not the vertex group of any graph with vertices. Various types and measures of symmetry of a graph can be related to its automorphisms. A graph with no automorphisms other than the identical one is said to be asymmetric. If 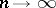, almost all graphs with vertices are asymmetric.

References

[1]	F. Harary, "Graph theory" , Addison-Wesley (1969) pp. Chapt. 9

Comments

The fact that for a finite group 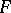there is a graph with automorphism group 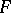is due to R. Frucht [a3]. A good reference for this and other algebraic aspects of graph theory is [a1]. A related reference is [a2].

References

[a1]	N. Biggs, "Algebraic graph theory" , Cambridge Univ. Press (1974)
[a2]	N. Biggs, "Finite groups of automorphisms" , Cambridge Univ. Press (1971)
[a3]	R. Frucht, "Herstellung von Graphen mit vorgegebener abstrakter Gruppe" Compos. Math. , 6 (1938) pp. 239–250