Graph, connectivity of a
One of the topological characteristics of a graph. A graph is said to be connected if for any two of its vertices  and
and  there exists a chain connecting these vertices. The vertex connectivity number of a graph
there exists a chain connecting these vertices. The vertex connectivity number of a graph 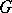 (denoted by
(denoted by 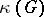 ) is the smallest number of vertices the removal of which results in a disconnected graph or in a graph consisting of one isolated vertex. The edge connectivity number (denoted by
) is the smallest number of vertices the removal of which results in a disconnected graph or in a graph consisting of one isolated vertex. The edge connectivity number (denoted by 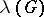 ) is the smallest number of edges of
) is the smallest number of edges of 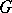 the removal of which results in a disconnected graph. A graph
the removal of which results in a disconnected graph. A graph 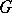 is said to be
is said to be 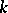 -connected if
-connected if 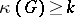 , and
, and  -edge-connected if
-edge-connected if 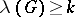 . A maximal
. A maximal 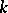 -connected subgraph of a graph
-connected subgraph of a graph 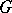 is said to be a
is said to be a 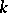 -connected component of it; a
-connected component of it; a 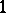 -connected component is called a connected component. In studying communication networks and logical networks, the connectivity numbers of the corresponding graphs can be interpreted as a degree of reliability of these networks.
-connected component is called a connected component. In studying communication networks and logical networks, the connectivity numbers of the corresponding graphs can be interpreted as a degree of reliability of these networks.
The theory of graphs studies methods for determining the connectivity of graphs, conditions under which a graph is 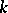 -connected or
-connected or 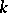 -edge-connected, the relations between the different types of connectivity, the dependence of the connectivity numbers on other graph parameters, etc. Thus, if
-edge-connected, the relations between the different types of connectivity, the dependence of the connectivity numbers on other graph parameters, etc. Thus, if 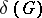 is the minimal degree of the vertices of a graph
is the minimal degree of the vertices of a graph 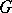 , the following inequalities are valid:
, the following inequalities are valid: 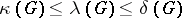 .
.
For any integers 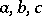 (
(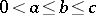 ) there exists a graph
) there exists a graph 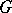 for which
for which 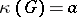 ,
, 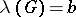 ,
, 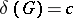 . If
. If 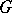 has
has  vertices and
vertices and 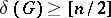 , then
, then 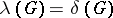 . One says that a set
. One says that a set 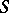 of vertices, edges, or vertices and edges separates two vertices
of vertices, edges, or vertices and edges separates two vertices  and
and  if
if  and
and  belong to different connected components of the graph
belong to different connected components of the graph 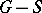 obtained from
obtained from 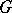 by the removal of the elements of
by the removal of the elements of 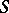 . The following statements are valid.
. The following statements are valid.
The smallest number of vertices separating two non-adjacent vertices  and
and  is equal to the largest number of simple chains without common vertices connecting
is equal to the largest number of simple chains without common vertices connecting  and
and  . A graph
. A graph 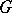 is
is 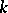 -connected if and only if any pair of its vertices is connected by at least
-connected if and only if any pair of its vertices is connected by at least 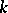 chains which do not intersect at the vertices. Similar theorems are also valid for edge connectivity. A graph is
chains which do not intersect at the vertices. Similar theorems are also valid for edge connectivity. A graph is 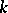 -edge-connected if and only if any pair of its vertices is connected by at least
-edge-connected if and only if any pair of its vertices is connected by at least 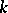 chains which do not intersect at the edges. A set of edges whose removal results in the formation of a disconnected graph is known as a cut. In each graph the largest number of cuts which do not intersect at the edges and which separate two vertices
chains which do not intersect at the edges. A set of edges whose removal results in the formation of a disconnected graph is known as a cut. In each graph the largest number of cuts which do not intersect at the edges and which separate two vertices  and
and  is equal to the smallest number of edges of a simple chain connecting
is equal to the smallest number of edges of a simple chain connecting  and
and  , i.e. to the distance
, i.e. to the distance 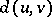 between
between  and
and  .
.
References
| [1] | F. Harary, "Graph theory" , Addison-Wesley (1969) pp. Chapt. 9 |
| [2] | L.R. Ford, D.R. Fulkerson, "Flows in networks" , Princeton Univ. Press (1962) |
Comments
The assertions in the last section can be derived from the maximum-flow-minimum-cut theorem of L. Ford and D. Fulkerson (see [2]). The first two are different versions of the vertex form of Menger's theorem (see [1]).
The maximum-flow-minimum-cut theorem, or the Ford–Fulkerson theorem, deals with a directed graph 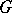 for which for each arc
for which for each arc  a capacity
a capacity 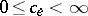 is specified. In addition, two special vertices, labeled
is specified. In addition, two special vertices, labeled 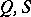 , are specified, called source and sink respectively, and there are no arcs leaving
, are specified, called source and sink respectively, and there are no arcs leaving  or entering
or entering 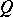 . A flow on the graph is given by specifying for every arc (i.e. directed edge) a number
. A flow on the graph is given by specifying for every arc (i.e. directed edge) a number 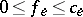 such that for every vertex
such that for every vertex 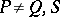 ,
,
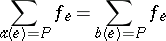 | (*) |
where for an arc  ,
, 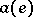 denotes its source vertex and
denotes its source vertex and 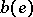 its target vertex. The maximum flow problem asks for a flow such that
its target vertex. The maximum flow problem asks for a flow such that
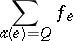 |
is maximized. In this setting a cut is a set of arcs whose removal results in a disconnected graph with 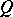 in one component and
in one component and 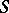 in another. The capacity of a cut is the sum of the capacities
in another. The capacity of a cut is the sum of the capacities 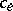 of the elements of the cut. The maximum-flow-minimum-cut theorem now says that the maximum flow attainable is equal to the minimal attainable capacity of a cut. The maximum flow problem can be formulated as a linear programming problem, and then the maximum-flow-minimum-cut theorem is an instance of the duality theorem of linear programming.
of the elements of the cut. The maximum-flow-minimum-cut theorem now says that the maximum flow attainable is equal to the minimal attainable capacity of a cut. The maximum flow problem can be formulated as a linear programming problem, and then the maximum-flow-minimum-cut theorem is an instance of the duality theorem of linear programming.
Recall that a chain in a non-oriented graph from 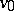 to
to 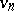 is a sequence
is a sequence 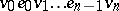 of alternating vertices and edges such that
of alternating vertices and edges such that 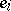 is an edge between
is an edge between 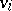 and
and 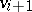 and such that all
and such that all 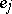 and all
and all 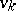 , except possibly
, except possibly 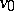 and
and 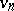 , are distinct. A
, are distinct. A 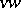 -disconnecting set or cut, where
-disconnecting set or cut, where 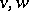 are two vertices, is a set of edges whose removal results in a disconnected graph with
are two vertices, is a set of edges whose removal results in a disconnected graph with  in one component and
in one component and 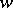 in another. The edge form of Menger's theorem now says that for a connected graph the maximum number of edge-disjoint chains from
in another. The edge form of Menger's theorem now says that for a connected graph the maximum number of edge-disjoint chains from  to
to 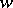 is equal to the minimum number of edges in a
is equal to the minimum number of edges in a 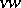 -disconnecting set. The theorem was in fact first proved by Ford and Fulkerson (1955). A
-disconnecting set. The theorem was in fact first proved by Ford and Fulkerson (1955). A 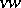 -separating set is a set of vertices
-separating set is a set of vertices 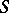 (not including
(not including  or
or 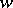 ) such that any chain from
) such that any chain from  to
to 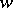 passes through
passes through 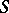 . The vertex form of Menger's theorem (Menger, 1928) now says that the maximum number of vertex-disjoint chains connecting distinct non-adjacent vertices
. The vertex form of Menger's theorem (Menger, 1928) now says that the maximum number of vertex-disjoint chains connecting distinct non-adjacent vertices  and
and 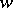 is equal to the minimal number of vertices in a
is equal to the minimal number of vertices in a 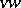 -separating set. Menger's theorem is closely related to the P. Hall marriage theorem; cf. Combinatorial analysis for that theorem.
-separating set. Menger's theorem is closely related to the P. Hall marriage theorem; cf. Combinatorial analysis for that theorem.
References
| [a1] | W.T. Tutte, "Connectivity in graphs" , Oxford Univ. Press (1966) |
| [a2] | R.J. Wilson, "Introduction to graph theory" , Longman (1985) |
| [a3] | H.-J. Walther, "Ten applications of graph theory" , Reidel (1984) pp. Sect. 6.1 |
Graph, connectivity of a. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Graph,_connectivity_of_a&oldid=12662