Grammar form
A (phrase-structure) grammar (cf. also Grammar system) 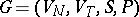 , viewed as a source of structurally similar grammars. (See Formal languages and automata.) The languages generated by the latter grammars give rise to a family
, viewed as a source of structurally similar grammars. (See Formal languages and automata.) The languages generated by the latter grammars give rise to a family 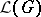 of languages. (See also Abstract family of languages.) Grammars viewed in this fashion, as generators of structurally similar grammars and their languages, are referred to as grammar forms.
of languages. (See also Abstract family of languages.) Grammars viewed in this fashion, as generators of structurally similar grammars and their languages, are referred to as grammar forms.
Let 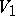 and
and 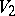 be alphabets. A disjoint-finite-letter substitution (dfl-substitution) is a mapping
be alphabets. A disjoint-finite-letter substitution (dfl-substitution) is a mapping 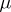 of
of 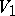 into the set of non-empty subsets of
into the set of non-empty subsets of 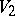 such that
such that 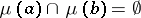 for all distinct
for all distinct  . Thus, a dfl-substitution associates one or more letters of
. Thus, a dfl-substitution associates one or more letters of 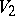 to each letter of
to each letter of  , and no letter of
, and no letter of 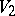 is associated to two letters of
is associated to two letters of 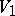 . Because
. Because 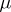 is a substitution, its domain is immediately extended to concern words and languages over
is a substitution, its domain is immediately extended to concern words and languages over 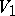 . For a production
. For a production 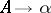 , one defines
, one defines
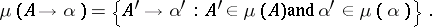 |
A grammar 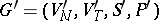 is an interpretation of a grammar
is an interpretation of a grammar 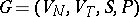 modulo
modulo 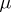 , denoted by
, denoted by 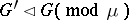 , where
, where 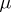 is a dfl-substitution on
is a dfl-substitution on 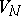 , if the following conditions are satisfied:
, if the following conditions are satisfied:
i) 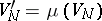 ,
, 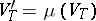 and
and 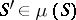 ;
;
ii) 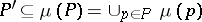 . The grammar
. The grammar 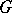 is referred to as the master or form grammar, while
is referred to as the master or form grammar, while 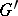 is the image or interpretation grammar. The grammar family and the grammatical (language) family of
is the image or interpretation grammar. The grammar family and the grammatical (language) family of 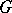 are defined by
are defined by
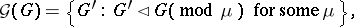 |
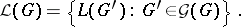 |
A language family 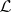 is termed grammatical if
is termed grammatical if 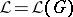 , for some
, for some 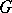 . Two grammars are form equivalent if their language families coincide. They are strongly form-equivalent if their grammar families coincide.
. Two grammars are form equivalent if their language families coincide. They are strongly form-equivalent if their grammar families coincide.
Operationally one obtains an interpretation grammar by mapping terminals and non-terminals of the form grammar into disjoint sets of terminals and non-terminals, respectively, then extending the mapping to concern productions and, finally, taking a subset of the resulting production set. The last-mentioned point is especially important: great flexibility results because it is possible to omit productions.
A grammar is said to be a grammar form if it is used within the framework of interpretations. There is no difference between a grammar and a grammar form as constructs.
Strong form equivalence is decidable, whereas form equivalence is undecidable even for context-free grammar forms. To characterize the grammar forms giving rise to a specific language family, e.g., the family of context-free languages, is equivalent to characterizing all possible normal forms for the corresponding grammars, e.g., all possible normal forms for context-free grammars. (For further details, see [a5]. [a1] and [a2] represent early developments.)
In spite of the discrete framework of formal languages, grammatical families possess remarkable density properties. For instance, if 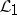 is a grammatical family containing all regular languages and
is a grammatical family containing all regular languages and 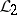 is a grammatical family such that
is a grammatical family such that 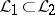 , then there is a grammatical family
, then there is a grammatical family 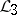 with the property
with the property 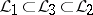 . (See [a3], [a4], [a5], and [a6] for a connection with graph colouring.) A theory analogous to grammar forms has been developed also for parallel rewriting. (See
. (See [a3], [a4], [a5], and [a6] for a connection with graph colouring.) A theory analogous to grammar forms has been developed also for parallel rewriting. (See 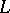 -systems, [a5].)
-systems, [a5].)
References
| [a1] | A.B. Cremers, S. Ginsburg, "Context-free grammar forms" J. Comput. System Sci. , 11 (1975) pp. 86–116 |
| [a2] | H.A. Maurer, M. Penttonen, A. Salomaa, D. Wood, "On non context-free grammar forms" Math. Systems Th. , 12 (1979) pp. 297–324 |
| [a3] | A. Salomaa, H.A. Maurer, D. Wood, "Dense hierarchies of grammatical families" J. Assoc. Comput. Mach. , 29 (1982) pp. 118–126 |
| [a4] | V. Niemi, "Density of grammar forms, I; II" Internat. J. Comput. Math. , 20 (1986) pp. 3–21; 91–114 |
| [a5] | Gh. Păun, A. Salomaa, "Families generated by grammars and L systems" G. Rozenberg (ed.) A. Salomaa (ed.) , Handbook of Formal Languages , 1 , Springer (1997) pp. 811–861 |
| [a6] | A. Salomaa, "On color-families of graphs" Ann. Acad. Sci. Fennicae , AI6 (1981) pp. 135–148 |
Grammar form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Grammar_form&oldid=11873