Gram matrix
From Encyclopedia of Mathematics
The square matrix
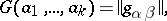 |
consisting of pairwise scalar products  of elements (vectors) of a (pre-)Hilbert space. All Gram matrices are non-negative definite. The matrix is positive definite if
of elements (vectors) of a (pre-)Hilbert space. All Gram matrices are non-negative definite. The matrix is positive definite if  are linearly independent. The converse is also true: Any non-negative (positive) definite
are linearly independent. The converse is also true: Any non-negative (positive) definite  -matrix is a Gram matrix (with linearly independent defining vectors).
-matrix is a Gram matrix (with linearly independent defining vectors).
If  are
are  -dimensional vectors (columns) of an
-dimensional vectors (columns) of an  -dimensional Euclidean (Hermitian) space with the ordinary scalar product
-dimensional Euclidean (Hermitian) space with the ordinary scalar product
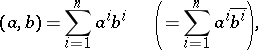 |
then
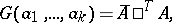 |
where  is the
is the 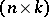 -matrix consisting of the columns
-matrix consisting of the columns  . The symbol
. The symbol  denotes the operation of matrix transposition, while the bar denotes complex conjugation of the variable. See also Gram determinant.
denotes the operation of matrix transposition, while the bar denotes complex conjugation of the variable. See also Gram determinant.
Comments
References
| [a1] | H. Schwerdtfeger, "Introduction to linear algebra and the theory of matrices" , Noordhoff (1950) (Translated from German) |
How to Cite This Entry:
Gram matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gram_matrix&oldid=19116
Gram matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gram_matrix&oldid=19116
This article was adapted from an original article by L.P. Kuptsov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article