Gram-Charlier series
A series defined by the expression
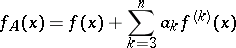 | (1) |
or
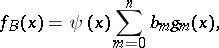 | (2) |
where  is the normalized value of a random variable.
is the normalized value of a random variable.
The series (1) is known as the Gram–Charlier series of type  ; here
; here
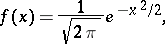 |
 is the
is the  -th derivative of
-th derivative of  , which can be represented as
, which can be represented as
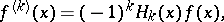 |
where  are the Chebyshev–Hermite polynomials. The derivatives
are the Chebyshev–Hermite polynomials. The derivatives  and the polynomials
and the polynomials  are orthogonal, owing to which the coefficients
are orthogonal, owing to which the coefficients  can be defined by the basic moments
can be defined by the basic moments  of the given distribution series. If one restricts to the first few terms of the series (1), one obtains
of the given distribution series. If one restricts to the first few terms of the series (1), one obtains
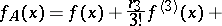 |
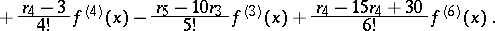 |
The series (2) is known as a Gram–Charlier series of type  ; here
; here
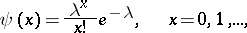 |
while  are polynomials analogous to the polynomials
are polynomials analogous to the polynomials  .
.
If one restricts to the first terms of the series (2), one obtains
 |
 |
Here  are the central moments of the distribution, while
are the central moments of the distribution, while  .
.
Gram–Charlier series were obtained by J.P. Gram [1] and C.V.L. Charlier [2] in their study of functions of the form
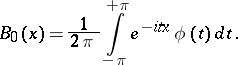 |
These are convenient for the interpolation between the values  of the general term of the binomial distribution, where
of the general term of the binomial distribution, where
 |
is the characteristic function of the binomial distribution. The expansion of  in powers of
in powers of  yields a Gram–Charlier series of type
yields a Gram–Charlier series of type  for
for  , whereas the expansion of
, whereas the expansion of  in powers of
in powers of  yields a Gram–Charlier series of type
yields a Gram–Charlier series of type  .
.
References
| [1] | J.P. Gram, "Ueber die Entwicklung reeller Funktionen in Reihen mittelst der Methode der kleinsten Quadraten" J. Reine Angew. Math. , 94 (1883) pp. 41–73 |
| [2] | C.V.L. Charlier, "Frequency curves of type  in heterograde statistics" Ark. Mat. Astr. Fysik , 9 : 25 (1914) pp. 1–17 in heterograde statistics" Ark. Mat. Astr. Fysik , 9 : 25 (1914) pp. 1–17 |
| [3] | A.K. Mitropol'skii, "Curves of distributions" , Leningrad (1960) (In Russian) |
Comments
Cf. also Edgeworth series.
References
| [a1] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) pp. Sect. 17.6 |
Gram-Charlier series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gram-Charlier_series&oldid=18126