Difference between revisions of "Goryachev-Chaplygin top"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | g1101701.png | ||
| + | $#A+1 = 16 n = 1 | ||
| + | $#C+1 = 16 : ~/encyclopedia/old_files/data/G110/G.1100170 Goryachev\ANDChaplygin top | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
A rigid body rotating about a fixed point, for which: | A rigid body rotating about a fixed point, for which: | ||
| − | a) the principal moments of inertia | + | a) the principal moments of inertia $ \lambda = ( \lambda _ {1} , \lambda _ {2} , \lambda _ {3} ) $, |
| + | with regard to the fixed point, satisfy the relation $ \lambda _ {1} = \lambda _ {2} = 4 \lambda _ {3} $; | ||
b) the centre of mass belongs to the equatorial plane through the fixed point; | b) the centre of mass belongs to the equatorial plane through the fixed point; | ||
| − | c) the principal angular momentum is perpendicular to the direction of gravity, i.e., | + | c) the principal angular momentum is perpendicular to the direction of gravity, i.e., $ \langle {m, \gamma } \rangle = 0 $. |
| + | First introduced by D. Goryachev [[#References|[a4]]] in 1900, the system was later integrated by S.A. Chaplygin [[#References|[a3]]] in terms of hyper-elliptic integrals (cf. also [[Hyper-elliptic integral|Hyper-elliptic integral]]). The system merely satisfying a) and b) is not algebraically integrable, but on the locus, defined by c), it is; namely, it has an extra invariant of homogeneous degree $ 3 $: | ||
| + | |||
| + | $$ | ||
| + | Q _ {4} = ( m ^ {2} _ {1} + m _ {2} ^ {2} ) m _ {3} + 2m _ {1} \gamma _ {3} . | ||
| + | $$ | ||
| + | |||
| + | C. Bechlivanidis and P. van Moerbeke [[#References|[a1]]] have shown that the problem has asymptotic solutions which are meromorphic in $ \sqrt t $; | ||
| + | the system linearizes on a double cover of a hyper-elliptic Jacobian (i.e., of the [[Jacobi variety|Jacobi variety]] of a [[Hyper-elliptic curve|hyper-elliptic curve]]; cf. also [[Plane real algebraic curve|Plane real algebraic curve]]), ramified exactly along the two hyper-elliptic curves, where the phase variables blow up; see also [[#References|[a5]]]. An elementary algebraic mapping transforms the Goryachev–Chaplygin equations into equations closely related to the $ 3 $- | ||
| + | body Toda lattice. A Lax pair is given in [[#References|[a2]]]: | ||
| + | |||
| + | $$ | ||
| + | - { | ||
| + | \frac{i}{2} | ||
| + | } ( { {h _ {- 1 } } tilde } h ^ {- 1 } + { {L _ {0} } tilde } + { {L _ {1} } tilde } h ) ^ \bullet = | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | = | ||
| + | [ { {L _ {- 1 } } tilde } h ^ {- 1 } + { {L _ {0} } tilde } + { {L _ {1} } tilde } h, { {B _ {0} } tilde } - { {L _ {1} } tilde } h ] , | ||
| + | $$ | ||
| − | + | where $ { {L _ {0} } tilde } $ | |
| + | and $ { {L _ {1} } tilde } $ | ||
| + | are given by the $ ( 3 \times 3 ) $ | ||
| + | right-lower corner of $ L _ {0} $ | ||
| + | and $ L _ {1} $ | ||
| + | and where | ||
| − | + | $$ | |
| + | { {L _ {- 1 } } tilde } = { | ||
| + | \frac{1}{2} | ||
| + | } \left ( | ||
| − | + | \begin{array}{ccc} | |
| + | 0 &- y _ {3} & 0 \\ | ||
| + | y _ {3} & 0 &y _ {1} - x _ {1} ^ {2} \\ | ||
| + | 0 &- y _ {2} + x _ {2} ^ {2} & 0 \\ | ||
| + | \end{array} | ||
| − | + | \right ) , | |
| + | $$ | ||
| − | + | $$ | |
| + | { {B _ {0} } tilde } = \left ( | ||
| − | + | \begin{array}{ccc} | |
| + | { | ||
| + | \frac{3}{2} | ||
| + | } x _ {3} & 0 &- x _ {1} \\ | ||
| + | 0 &{ | ||
| + | \frac{3}{2} | ||
| + | } x _ {3} & 0 \\ | ||
| + | - x _ {2} & 0 &- x _ {3} \\ | ||
| + | \end{array} | ||
| − | + | \right ) . | |
| + | $$ | ||
See also [[Kowalewski top|Kowalewski top]]. | See also [[Kowalewski top|Kowalewski top]]. | ||
Latest revision as of 19:42, 5 June 2020
A rigid body rotating about a fixed point, for which:
a) the principal moments of inertia $ \lambda = ( \lambda _ {1} , \lambda _ {2} , \lambda _ {3} ) $, with regard to the fixed point, satisfy the relation $ \lambda _ {1} = \lambda _ {2} = 4 \lambda _ {3} $;
b) the centre of mass belongs to the equatorial plane through the fixed point;
c) the principal angular momentum is perpendicular to the direction of gravity, i.e., $ \langle {m, \gamma } \rangle = 0 $. First introduced by D. Goryachev [a4] in 1900, the system was later integrated by S.A. Chaplygin [a3] in terms of hyper-elliptic integrals (cf. also Hyper-elliptic integral). The system merely satisfying a) and b) is not algebraically integrable, but on the locus, defined by c), it is; namely, it has an extra invariant of homogeneous degree $ 3 $:
$$ Q _ {4} = ( m ^ {2} _ {1} + m _ {2} ^ {2} ) m _ {3} + 2m _ {1} \gamma _ {3} . $$
C. Bechlivanidis and P. van Moerbeke [a1] have shown that the problem has asymptotic solutions which are meromorphic in $ \sqrt t $; the system linearizes on a double cover of a hyper-elliptic Jacobian (i.e., of the Jacobi variety of a hyper-elliptic curve; cf. also Plane real algebraic curve), ramified exactly along the two hyper-elliptic curves, where the phase variables blow up; see also [a5]. An elementary algebraic mapping transforms the Goryachev–Chaplygin equations into equations closely related to the $ 3 $- body Toda lattice. A Lax pair is given in [a2]:
$$ - { \frac{i}{2} } ( { {h _ {- 1 } } tilde } h ^ {- 1 } + { {L _ {0} } tilde } + { {L _ {1} } tilde } h ) ^ \bullet = $$
$$ = [ { {L _ {- 1 } } tilde } h ^ {- 1 } + { {L _ {0} } tilde } + { {L _ {1} } tilde } h, { {B _ {0} } tilde } - { {L _ {1} } tilde } h ] , $$
where $ { {L _ {0} } tilde } $ and $ { {L _ {1} } tilde } $ are given by the $ ( 3 \times 3 ) $ right-lower corner of $ L _ {0} $ and $ L _ {1} $ and where
$$ { {L _ {- 1 } } tilde } = { \frac{1}{2} } \left ( \begin{array}{ccc} 0 &- y _ {3} & 0 \\ y _ {3} & 0 &y _ {1} - x _ {1} ^ {2} \\ 0 &- y _ {2} + x _ {2} ^ {2} & 0 \\ \end{array} \right ) , $$
$$ { {B _ {0} } tilde } = \left ( \begin{array}{ccc} { \frac{3}{2} } x _ {3} & 0 &- x _ {1} \\ 0 &{ \frac{3}{2} } x _ {3} & 0 \\ - x _ {2} & 0 &- x _ {3} \\ \end{array} \right ) . $$
See also Kowalewski top.
References
| [a1] | C. Bechlivanidis, P. van Moerbeke, "The Goryachev–Chaplygin top and the Toda lattice" Comm. Math. Phys. , 110 (1987) pp. 317–324 |
| [a2] | A.I. Bobenko, V.B. Kuznetsov, "Lax representation and new formulae for the Goryachev–Chaplygin top" J. Phys. A , 21 (1988) pp. 1999–2006 |
| [a3] | S.A. Chaplygin, "A new case of rotation of a rigid body, supported at one point" , Collected works , I , Gostekhizdat (1948) pp. 118–124 (In Russian) |
| [a4] | D. Goryachev, "On the motion of a rigid material body about a fixed point in the case 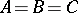 " Mat. Sb. , 21 (1900) (In Russian) " Mat. Sb. , 21 (1900) (In Russian) |
| [a5] | L. Piovan, "Cyclic coverings of Abelian varieties and the Goryachev–Chaplygin top" Math. Ann. , 294 (1992) pp. 755–764 |
Goryachev-Chaplygin top. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Goryachev-Chaplygin_top&oldid=14870