Goppa code
Let 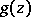 be a monic polynomial over the finite field
be a monic polynomial over the finite field 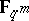 and let
and let 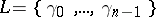 be a set of
be a set of  elements of
elements of 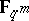 such that
such that 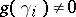 for
for 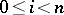 . The classical Goppa code
. The classical Goppa code 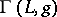 with Goppa polynomial
with Goppa polynomial 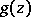 is the set of all words
is the set of all words 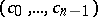 in
in 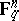 for which
for which 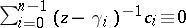
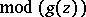 . Here
. Here 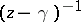 is to be interpreted as
is to be interpreted as 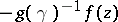 where
where 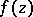 is the unique polynomial of degree
is the unique polynomial of degree  degree
degree 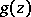 such that
such that 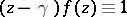
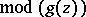 .
.
The basic idea of this construction can be generalized as follows. Let 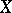 be a non-singular projective curve (in the sense of algebraic geometry) defined over the finite field
be a non-singular projective curve (in the sense of algebraic geometry) defined over the finite field 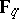 . Let
. Let 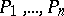 be a set of rational points of
be a set of rational points of 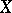 . Let
. Let 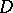 be the divisor
be the divisor 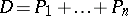 . Let
. Let 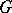 be another divisor with support disjoint from
be another divisor with support disjoint from 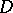 . Let
. Let 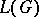 be the linear system associated to the divisor
be the linear system associated to the divisor 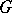 , i.e.
, i.e. 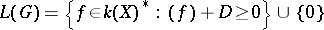 , where
, where 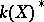 is the set of non-zero rational functions on
is the set of non-zero rational functions on 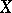 and
and 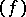 is the divisor of zeros and poles defined by an
is the divisor of zeros and poles defined by an 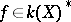 . The geometric Goppa code
. The geometric Goppa code 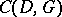 of length
of length  associated to the pair
associated to the pair 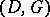 is the image of the linear mapping
is the image of the linear mapping 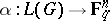 defined by
defined by 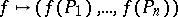 . If the supports of
. If the supports of 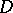 and
and  are not disjoint, there is still a code associated to the pair
are not disjoint, there is still a code associated to the pair 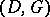 , but not a canonical one; however, all the codes so obtained are equivalent in a suitable sense. A second code associated to the pair
, but not a canonical one; however, all the codes so obtained are equivalent in a suitable sense. A second code associated to the pair 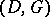 is the following. Let
is the following. Let 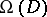 be the vector space of rational differential forms
be the vector space of rational differential forms 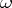 on
on 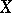 with
with 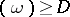 , with the zero form added. The second linear code
, with the zero form added. The second linear code 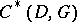 associated to the pair
associated to the pair 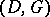 is the image of the linear mapping
is the image of the linear mapping 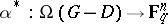 defined by
defined by 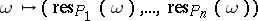 . This is the construction which more directly generalizes the classical Goppa codes mentioned above. The codes
. This is the construction which more directly generalizes the classical Goppa codes mentioned above. The codes 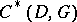 and
and 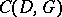 are dual to each other. For fixed
are dual to each other. For fixed 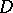 and varying
and varying 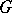 the codes
the codes 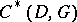 and
and 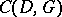 yield the same family.
yield the same family.
At present (1989) one approach to finding good codes is to find curves with large numbers of rational points compared to their genus. This brings in advanced algebraic geometry. Using Shimura curves (modular curves) one now can find a sequence of codes which beats the Gilbert–Varshamov bound for  . For more details cf. [a4], [a7]–[a9].
. For more details cf. [a4], [a7]–[a9].
References
| [a1] | J.H. van Lint, "Introduction to coding theory" , Springer (1982) |
| [a2] | A. Tietäväinen, "On the non-existence of perfect codes over finite fields" SIAM J. Appl. Math. , 24 (1973) pp. 88–96 |
| [a3] | R.J. McEliece, E.R. Rodemich, H. Rumsey, L.R. Welch, "New upper bounds on the rate of a code via the Delsarte–MacWilliams inequalities" IEEE Trans. Inform. Theory , 23 (1977) pp. 157–166 |
| [a4] | M.A. Tsfasman, S.G. Vladuts, T. Zink, "Modular curves, Shimura curves and Goppa codes, better than Varshamov–Gilbert bound" Math. Nachr. , 109 (1982) pp. 21–28 |
| [a5] | P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) (Updated reprint) |
| [a6] | R. Hill, "A first course in coding theory" , Clarendon Press (1986) |
| [a7] | J.H. van Lint, G. van der Geer, "Introduction to coding theory and algebraic geometry" , Birkhäuser (1988) |
| [a8] | V.D. Goppa, "Geometry and codes" , Kluwer (1988) |
| [a9] | M.A. Tsfasman, S.G. Vlăduts, "Algebraic geometric codes" , Kluwer (1989) |
Goppa code. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Goppa_code&oldid=17352