Difference between revisions of "Golden ratio"
(Importing text file) |
(picture remake) |
||
| Line 27: | Line 27: | ||
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457013.png" /> are the [[Fibonacci numbers|Fibonacci numbers]]. | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457013.png" /> are the [[Fibonacci numbers|Fibonacci numbers]]. | ||
| − | < | + | <center><asy> |
| − | + | pair A=(-1,0); | |
| + | pair B=(0,0); | ||
| + | pair E=(0,0.5); | ||
| + | pair C=A+(0.5*(sqrt(5)-1),0); | ||
| + | pair D=(-1/sqrt(5), 0.5*(1-1/sqrt(5))); | ||
| + | |||
| + | draw( A--B--E--cycle,currentpen+1.5 ); | ||
| + | dot(A,currentpen+3.5); dot(B,currentpen+3.5); dot(E,currentpen+3.5); dot(C,currentpen+3.5); dot(D,currentpen+3.5); | ||
| + | |||
| + | draw( shift(E)*scale(0.5)*unitcircle,currentpen+1 ); | ||
| + | draw( shift(A)*scale(0.5*(sqrt(5)-1))*unitcircle,currentpen+1 ); | ||
| + | |||
| + | // draw( shift(B)*scale(0.5)*unitcircle, dashed+red ); | ||
| + | |||
| + | clip(A+(-0.15,-0.15)--B+(0.15,-0.15)--E+(0.15,0.15)--A+(-0.15,0.15)--cycle); | ||
| + | |||
| + | label("$A$",A,S); label("$B$",B,S); label("$C$",C,S); | ||
| + | label("$E$",E,N); label("$D$",D,N); | ||
| + | |||
| + | label( "\small Golden Ratio construction", (-0.5,0.8) ); | ||
| + | |||
| + | shipout(scale(100)*currentpicture); | ||
| + | </asy></center> | ||
The golden ratio of a segment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457014.png" /> may be found by a geometric construction (see Fig.). Draw the perpendicular to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457015.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457016.png" />; on the perpendicular, mark off the segment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457017.png" />; then join <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457019.png" />, mark off <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457020.png" /> and finally <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457021.png" />. Then | The golden ratio of a segment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457014.png" /> may be found by a geometric construction (see Fig.). Draw the perpendicular to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457015.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457016.png" />; on the perpendicular, mark off the segment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457017.png" />; then join <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457019.png" />, mark off <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457020.png" /> and finally <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044570/g04457021.png" />. Then | ||
Revision as of 16:25, 29 November 2014
golden section, sectio aurea, sectio divina, divina proportio, golden mean, harmonic division, division in extreme and mean ratio
The division of a line segment  into two parts the greater of which,
into two parts the greater of which,  , is the mean proportional between the whole segment
, is the mean proportional between the whole segment  and the smaller part
and the smaller part  , i.e.
, i.e.
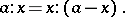 | (*) |
To find  , one has to solve a quadratic equation,
, one has to solve a quadratic equation,
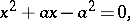 |
the positive solution of which is
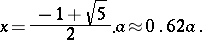 |
Condition (*) may also be written as
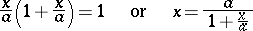 |
or
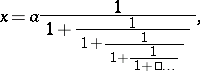 |
i.e. representing  as a continued fraction, the convergents of which are
as a continued fraction, the convergents of which are
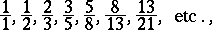 |
where 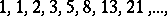 are the Fibonacci numbers.
are the Fibonacci numbers.
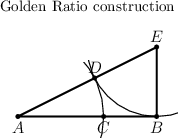
The golden ratio of a segment 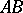 may be found by a geometric construction (see Fig.). Draw the perpendicular to
may be found by a geometric construction (see Fig.). Draw the perpendicular to 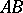 at
at 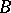 ; on the perpendicular, mark off the segment
; on the perpendicular, mark off the segment  ; then join
; then join 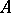 and
and 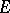 , mark off
, mark off 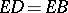 and finally
and finally 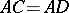 . Then
. Then
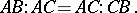 |
The golden ratio was already known in Antiquity. Its first appearance in the extant classical literature is in Euclid's Elements, Book II, 11 (3th century B.C.).
Principles based on the golden ratio or similar proportional ratios provided the basis for the compositional design of many works of art (mainly architectural works of Antiquity and the Renaissance).
Comments
The golden ratio occurs in many places in nature. It is assumed to have been known and used by the Pythagoreans (500 B.C.).
The term "divina proportio" (sectio divina, divine section) has been introduced by Fra Luca Pacioli in his book: De Divina Proportione (1509). Later on he collaborated with Leonardo da Vinci on this topic. The term "golden section" (sectio aurea) is from a later date (probably 18th century).
Golden ratio. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Golden_ratio&oldid=35088