Goldbach problem
One of the well-known problems in number theory: To give a proof that every odd integer equal to or larger than 7 can be written as the sum of three prime numbers. It was posed in 1742 by Ch. Goldbach in a communication to L. Euler. Euler replied by pointing out that in order to solve this problem it is sufficient to prove that every even number 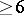 is the sum of two prime numbers. All attempts to solve the problem remained unsuccessful for a long time. G.H. Hardy and J.E. Littlewood in 1923 succeeded in showing that if certain theorems concerning Dirichlet
is the sum of two prime numbers. All attempts to solve the problem remained unsuccessful for a long time. G.H. Hardy and J.E. Littlewood in 1923 succeeded in showing that if certain theorems concerning Dirichlet 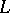 -function (which have not been proved till now) are valid, then any sufficiently large odd number is the sum of three prime numbers. I.M. Vinogradov in 1937 discovered a new method in analytic number theory — the method of estimating trigonometric sums involving prime numbers — and applied this method to prove an asymptotic formula for the number of representations of odd numbers as sums of three prime numbers (cf. Vinogradov method; Trigonometric sums, method of). This formula implies that each sufficiently large odd number is the sum of three prime numbers. This is one of the major achievements of modern mathematics. Vinogradov's method offers a way for solving several problems of a much more general nature. The problem of writing every even number as a sum of two prime numbers has not yet (1989) been solved.
-function (which have not been proved till now) are valid, then any sufficiently large odd number is the sum of three prime numbers. I.M. Vinogradov in 1937 discovered a new method in analytic number theory — the method of estimating trigonometric sums involving prime numbers — and applied this method to prove an asymptotic formula for the number of representations of odd numbers as sums of three prime numbers (cf. Vinogradov method; Trigonometric sums, method of). This formula implies that each sufficiently large odd number is the sum of three prime numbers. This is one of the major achievements of modern mathematics. Vinogradov's method offers a way for solving several problems of a much more general nature. The problem of writing every even number as a sum of two prime numbers has not yet (1989) been solved.
References
| [1] | I.M. Vinogradov, "The method of trigonometric sums in the theory of numbers" , Interscience (1954) (Translated from Russian) |
| [2] | A.A. Karatsuba, "Fundamentals of analytic number theory" , Moscow (1975) (In Russian) |
Comments
In [a1] a concise proof can be found of Vinogradov's result on the ternary Goldbach problem. In 1973 Chen Jing-run proved that every sufficiently large even number is a sum of a prime and a number composed of at most two primes. For a proof see [a2], Chapt. 11.
In [a3] Goldbach's conjecture (in the form 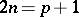 ,
, 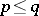 ) is studied from a numerical point of view. Special attention is devoted to the smallest
) is studied from a numerical point of view. Special attention is devoted to the smallest 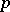 for which
for which  . It was found that
. It was found that 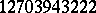 is the worst case in the range
is the worst case in the range 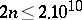 , i.e. this number can be written as
, i.e. this number can be written as 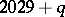 whereas every other
whereas every other 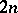 not exceeding
not exceeding 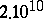 has a representation
has a representation 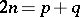 with
with 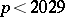 .
.
References
| [a1] | R.C. Vaughan, "The Hardy–Littlewood method" , Cambridge Univ. Press (1981) |
| [a2] | H. Halberstam, H.-E. Richert, "Sieve methods" , Acad. Press (1974) |
| [a3] | A. Granville, J. van der Lune, H.J.J. te Riele, "Checking the Goldbach conjecture on a vector computer" R.A. Molin (ed.) , Number theory and applications (Proc. First Conf. Canadian Number Theory Assoc., Banff, April 1988) , Kluwer (1989) ((Also: Mathematical Centre Report NM R8812 (1988))) |
| [a4] | Wang Yuan (ed.) , Goldbach conjecture , World Sci. (1984) |
Goldbach problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Goldbach_problem&oldid=14884