Glueing method
in the theory of surfaces
A method for constructing surfaces isometric to a given one. The glueing method has applications in proving the realizability of abstractly-defined convex metrics, in questions of bending convex surfaces, and in quantitative estimates of bendability. Its strength lies in the fact that it works in situations where differential equations are powerless.
Aleksandrov's theorem: Let 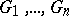 be closed domains in a manifold with an intrinsic metric of positive curvature, bounded by a finite number of curves with bounded rotational variation. Let
be closed domains in a manifold with an intrinsic metric of positive curvature, bounded by a finite number of curves with bounded rotational variation. Let 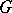 be the manifold consisting of the domains
be the manifold consisting of the domains 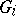 with their boundaries identified in such a way that:
with their boundaries identified in such a way that:
1) the identified segments of the boundaries of 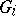 and
and 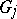 have equal length;
have equal length;
2) the sum of the rotations of the identified segments of the boundaries of 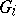 and
and 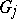 from the sides of these domains is non-negative;
from the sides of these domains is non-negative;
3) the sum of the angles made by the sectors at the identified points of the domains 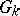 with the sides of these domains does not exceed
with the sides of these domains does not exceed 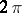 .
.
Then 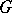 has an intrinsic metric of positive curvature that coincides with the metrics of the domains in neighbourhoods of corresponding points.
has an intrinsic metric of positive curvature that coincides with the metrics of the domains in neighbourhoods of corresponding points.
References
| [1] | A.D. Aleksandrov, V.A. Zalgaller, "Two-dimensional manifolds of bounded curvature" Proc. Steklov Inst. Math. , 76 (1962) Trudy Mat. Inst. Steklov. , 76 (1962) |
| [2] | A.V. Pogorelov, "Die Verbiegung konvexer Flächen" , Akademie Verlag (1957) (Translated from Russian) |
Glueing method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Glueing_method&oldid=18059