Global structure of trajectories
of a quadratic differential
A description of the behaviour as a whole of trajectories of a positive quadratic differential on a compact oriented Riemann surface (cf. Quadratic differential for the definition of trajectory in this setting). Let 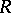 be a compact oriented Riemann surface, let
be a compact oriented Riemann surface, let 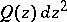 be a positive quadratic differential on
be a positive quadratic differential on 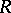 , let
, let 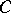 be the set of all zeros and simple poles of
be the set of all zeros and simple poles of 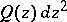 , and let
, and let 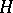 be the set of poles of
be the set of poles of 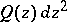 of order
of order  . The trajectories of
. The trajectories of 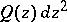 form a family
form a family 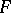 which has many of the properties of regular families of curves. This family of curves covers
which has many of the properties of regular families of curves. This family of curves covers 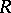 except for the points of the set
except for the points of the set 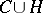 , i.e. through every point of
, i.e. through every point of 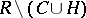 passes a unique element of
passes a unique element of 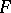 . The behaviour of a trajectory of
. The behaviour of a trajectory of 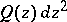 in a neighbourhood of any point of
in a neighbourhood of any point of 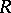 is described by the local structure of the trajectories of the quadratic differential (cf. Local structure of trajectories). In considering the global structure of the curves of
is described by the local structure of the trajectories of the quadratic differential (cf. Local structure of trajectories). In considering the global structure of the curves of 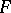 at the points of
at the points of 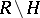 , an important role is played by the following unions of trajectories. Let
, an important role is played by the following unions of trajectories. Let 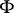 be the union of all trajectories of
be the union of all trajectories of 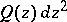 having limit end points at some point of
having limit end points at some point of 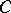 ; let
; let 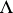 be the subset of
be the subset of  that is the union of all the trajectories of
that is the union of all the trajectories of 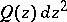 which have one limit end point at a point of
which have one limit end point at a point of 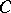 and a second limit end point at a point of
and a second limit end point at a point of 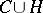 .
.
A set  on
on 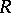 is called an
is called an 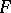 -set with respect to
-set with respect to 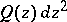 if each trajectory of
if each trajectory of  intersecting with
intersecting with 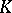 is completely contained in
is completely contained in 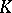 . The internal closure of the set
. The internal closure of the set 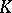 is defined as the interior of the closure
is defined as the interior of the closure 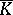 and is denoted by
and is denoted by 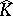 . The internal closure of an
. The internal closure of an 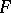 -set is also an
-set is also an 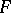 -set. The terminal domain
-set. The terminal domain 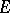 with respect to
with respect to 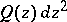 is the largest connected open
is the largest connected open 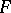 -set on
-set on  with the following properties: 1)
with the following properties: 1) 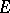 contains no points of
contains no points of 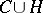 ; 2)
; 2) 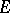 is filled with trajectories of
is filled with trajectories of 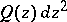 , each one of which has a limit end point in each one of the two possible directions at a given point
, each one of which has a limit end point in each one of the two possible directions at a given point 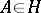 ; and 3)
; and 3) 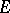 is conformally mapped by the function
is conformally mapped by the function
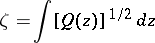 |
onto the left or right half-plane of the 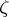 -plane (depending on the choice of the branch of the root). It follows from the local structure of the trajectories of
-plane (depending on the choice of the branch of the root). It follows from the local structure of the trajectories of 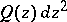 that the point
that the point 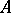 should be a pole of the differential
should be a pole of the differential 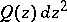 of order at least three.
of order at least three.
The strip-like domain  with respect to
with respect to 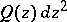 is the largest connected open
is the largest connected open  -set on
-set on  with the following properties: 1)
with the following properties: 1) 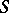 contains no points of
contains no points of 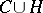 ; 2)
; 2) 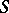 is filled with the trajectories of
is filled with the trajectories of 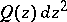 , each one of which has at one point
, each one of which has at one point  a limit end point in one direction and at another point
a limit end point in one direction and at another point 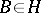 (which may coincide with
(which may coincide with  ) a limit end point in the other direction; and 3)
) a limit end point in the other direction; and 3) 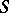 is conformally mapped by the function
is conformally mapped by the function
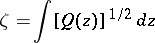 |
onto the strip 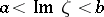 , where
, where  and
and 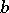 are finite real numbers and
are finite real numbers and 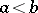 . The points
. The points  and
and 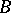 may be poles of
may be poles of 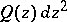 of order two or larger.
of order two or larger.
The circular domain 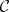 with respect to
with respect to 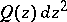 is the largest connected open
is the largest connected open 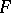 -set on
-set on 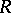 with the following properties: 1)
with the following properties: 1) 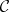 contains a unique double pole
contains a unique double pole 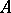 of
of 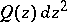 ; 2)
; 2) 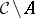 is filled with the trajectories of
is filled with the trajectories of 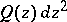 each one of which is a closed Jordan curve which separates
each one of which is a closed Jordan curve which separates 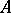 from the boundary of
from the boundary of 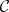 ; and 3) if a purely-imaginary constant
; and 3) if a purely-imaginary constant  has been suitably chosen, the function
has been suitably chosen, the function
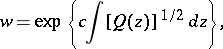 |
supplemented by the value zero at 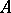 , conformally maps
, conformally maps 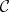 onto a disc
onto a disc 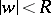 , and
, and 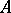 is mapped to
is mapped to 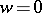 .
.
The annular domain 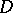 with respect to
with respect to 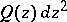 is the largest connected
is the largest connected 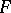 -set on
-set on 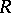 with the following properties: 1)
with the following properties: 1)  does not contain any points of
does not contain any points of 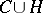 ; 2)
; 2) 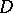 is filled with trajectories of
is filled with trajectories of 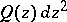 each one of which is a closed Jordan curve; and 3) if a purely-imaginary constant
each one of which is a closed Jordan curve; and 3) if a purely-imaginary constant  is suitably chosen, the function
is suitably chosen, the function
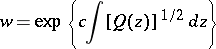 |
conformally maps 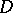 onto a circular annulus
onto a circular annulus 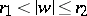 ,
, 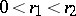 .
.
The dense domain 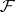 with respect to
with respect to 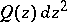 is the largest connected
is the largest connected 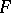 -set on
-set on 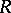 with the following properties: 1)
with the following properties: 1) 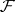 does not contain any points of
does not contain any points of 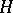 ; and 2)
; and 2) 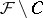 is filled with trajectories of
is filled with trajectories of 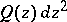 , each one of which is everywhere-dense in
, each one of which is everywhere-dense in 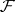 .
.
The basic structure theorem is valid [2]. Let 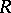 be a compact oriented Riemann surface and let
be a compact oriented Riemann surface and let 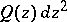 be a positive quadratic differential on
be a positive quadratic differential on 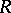 , while excluding the following possible cases and all configurations obtainable from such cases by way of a conformal mapping: I.
, while excluding the following possible cases and all configurations obtainable from such cases by way of a conformal mapping: I. 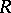 is a
is a  -sphere,
-sphere, 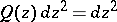 ; II.
; II. 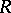 is a
is a  -sphere,
-sphere, 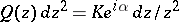 ,
, 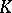 being positive and
being positive and 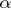 being a real number; and III.
being a real number; and III. 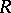 is a torus, and
is a torus, and 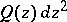 is regular on
is regular on 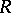 . Then 1)
. Then 1) 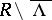 consists of a finite number of terminal, strip-like, annular, and dense domains; 2) each such domain is bounded by a finite number of trajectories together with points at which the latter meet; each boundary component of such a domain contains a point of
consists of a finite number of terminal, strip-like, annular, and dense domains; 2) each such domain is bounded by a finite number of trajectories together with points at which the latter meet; each boundary component of such a domain contains a point of 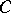 , except for boundary components of the circular or annular domain which may coincide with a boundary components of
, except for boundary components of the circular or annular domain which may coincide with a boundary components of 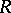 ; for a strip-like domain two boundary elements issuing from points of the set
; for a strip-like domain two boundary elements issuing from points of the set 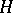 subdivide the boundary into two parts, each one of which contains a point of the set
subdivide the boundary into two parts, each one of which contains a point of the set 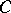 ; 3) each pole of
; 3) each pole of 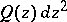 of order
of order 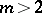 has a neighbourhood that can be covered by the internal closure of the union of
has a neighbourhood that can be covered by the internal closure of the union of 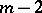 terminal domains and a finite number (which may also be equal to zero) of strip-like domains; and 4) each pole of
terminal domains and a finite number (which may also be equal to zero) of strip-like domains; and 4) each pole of 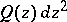 of order
of order 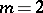 has a neighbourhood that can be covered by the internal closure of the union of a finite number of strip-like domains, or has a neighbourhood contained in a circular domain.
has a neighbourhood that can be covered by the internal closure of the union of a finite number of strip-like domains, or has a neighbourhood contained in a circular domain.
The statement of the basic structure theorem of J.A. Jenkins [1] in its original formulation immediately follows from this theorem: Under the conditions of the theorem the set  consists of a finite number of terminal, strip-like, circular, and annular domains. In a number of studies in the theory of univalent functions, main stress is laid on proving the fact that the set
consists of a finite number of terminal, strip-like, circular, and annular domains. In a number of studies in the theory of univalent functions, main stress is laid on proving the fact that the set 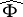 is empty for the quadratic differential
is empty for the quadratic differential 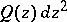 under consideration. The search for conditions under which
under consideration. The search for conditions under which 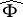 is empty is also of interest in its own right. The following three-pole theorem provides an example of a quadratic differential
is empty is also of interest in its own right. The following three-pole theorem provides an example of a quadratic differential 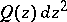 on the
on the  -sphere for which the set
-sphere for which the set 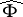 is empty: If
is empty: If 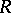 is the
is the  -sphere and
-sphere and 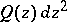 is a quadratic differential on
is a quadratic differential on 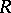 with at most three different poles, then
with at most three different poles, then 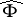 is empty.
is empty.
References
| [1] | J.A. Jenkins, "Univalent functions and conformal mappings" , Springer (1958) |
| [2] | J.A. Jenkins, "On the global structure of the trajectories of a positive quadratic differential" Illinois J. Math. , 4 : 3 (1960) pp. 405–412 |
Global structure of trajectories. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Global_structure_of_trajectories&oldid=11891