Geophysics, mathematical problems in
Problems that arise in the analysis of physical phenomena in studies of the structure of the Earth. Depending on the nature of the physical phenomena involved, one distinguishes between the following types of geophysical studies: gravitational exploration, based on the study of the gravity field; magnetic exploration, based on the study of the static magnetic field; seismic exploration, based on the study of the propagation of elastic waves; electromagnetic probing, based on the study of the fields produced by stationary currents or alternating electromagnetic fields; and nuclear prospecting, based on changes in the intensity in radiation of the natural or induced radioactivity of rocks. The fields may be determined on the Earth's surface (surface methods), in the air (aero-prospecting) and in boreholes (subsurface methods and well logging) [1].
Similar mathematical problems arise in gravitational and magnetic prospecting. In both cases the primary problem consists of solving the Poisson equation
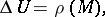 |
where  is the gravitational or magnetic potential, and
is the gravitational or magnetic potential, and 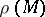 is the excess volume density of mass or the equivalent magnetic charges related to the magnetization of rocks. The quantity that is experimentally determined is
is the excess volume density of mass or the equivalent magnetic charges related to the magnetization of rocks. The quantity that is experimentally determined is 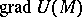 ; it determines either the variation of the acceleration of free fall
; it determines either the variation of the acceleration of free fall 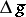 , or a change in the static magnetic field of the Earth. The measurements are conducted at various points on the surface of the Earth. These experimental data are then used to obtain the distribution of the function
, or a change in the static magnetic field of the Earth. The measurements are conducted at various points on the surface of the Earth. These experimental data are then used to obtain the distribution of the function 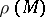 in the interior of the Earth. The direct task is simple, and the solution is obtained by quadratures. The principal difficulty consists in solving the inverse problem. Methods of the theory of harmonic fields and analytic continuation [2] are extensively used for this purpose.
in the interior of the Earth. The direct task is simple, and the solution is obtained by quadratures. The principal difficulty consists in solving the inverse problem. Methods of the theory of harmonic fields and analytic continuation [2] are extensively used for this purpose.
Problems arising in electromagnetic probing on stationary currents are of a somewhat different nature. Although the field is irrotational in this case, i.e. the electric field  is expressed in terms of the electric scalar potential
is expressed in terms of the electric scalar potential 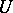 , the potential equation has the somewhat more complicated form
, the potential equation has the somewhat more complicated form
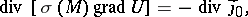 |
where  is the volume source density of electric current, while
is the volume source density of electric current, while 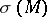 is the distribution of the conductivity in the Earth. The direct problem is to determine, on the surface of the Earth, the electric field for the various structural models of the medium (the distribution of
is the distribution of the conductivity in the Earth. The direct problem is to determine, on the surface of the Earth, the electric field for the various structural models of the medium (the distribution of 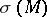 ). The inverse problem is to find the distribution of the conductivity
). The inverse problem is to find the distribution of the conductivity  from the experimental values of the electric field taken at different points of the Earth's surface.
from the experimental values of the electric field taken at different points of the Earth's surface.
Even more complex problems arise in the theory of electromagnetic probing in methods involving the use of alternating electromagnetic fields. The quantities that are experimentally determined in such methods are the components of these fields, the computation of which involves solving the Maxwell equations for inhomogeneous media, i.e. when the coefficients of the equations are position-depended functions. The inverse task consists in finding the coefficients of the equations from a known electromagnetic field. Several variants of experimental determinations are possible in such a case. The quantity being measured may be the non-stationary field at a single point as a function of time (time-domain probing of the medium), or a steady-state field of a given frequency as a function of the frequency (frequency-domain probing) but also as a function of the point of observation (array-probing) [3].
In seismic exploration the complete problem may be presented as the solution of the equation of propagation of elastic waves with space-depended coefficients under conditions of point excitation. This problem has been solved for the simplest models of medium structure only. However, in a number of cases the principal quantity that is experimentally determined in seismic exploration are the travel times of the reflected signals. Then a geometrical-optics approximation is employed, and the eikonal equation is solved in order to determine the trajectory of the ray, after which the travel time of the signal is computed. The travel times of the signal are determined at different points of the Earth's surface. The inverse problem consists in determining the boundary of the reflector from the known dependence of the travel time of the signal on the coordinates of the point of observation [4].
The principal objective of all geophysical investigations is the solution of the inverse problem, viz. the determination of the structure of the medium from the experimental values of the field quantities. The parameters that determine the structure of the medium are the coefficients of the partial differential equation or the right-hand sides of the equation that is satisfied by the field. The problem of finding the coefficients or the right-hand side of an equation the solution of which is known only in a certain part of the space is an ill-posed problem. For this reason, A.N. Tikhonov's regularization method [5] can profitably be employed in solving inverse problems in geophysics.
Regularization of the solution of inverse problems in geophysics consists of the selection of a sufficiently narrow class of solutions in which the problem becomes correct. This selection is carried out by constructing a family of mathematical models of the structure of the medium which, on one hand, describe the practical situations with sufficient accuracy and, on the other, are determined by a not too large number of model parameters. The principal mathematical problem involved in solving the inverse problems in geophysics in fact consists in the construction of mathematical models with allowance for the concrete realizations of various methods of geophysical investigations, while taking into account the objective of the particular investigation, and the development of effective algorithms for the solution of the direct problems for these models.
Once the family of mathematical models has been constructed, and the algorithm for solving the direct problem is known, the inverse problem can be generally formulated as follows. Let 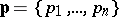 be the parameters of the model, and let
be the parameters of the model, and let 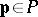 , where
, where 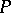 is the set of admissible values of the parameters of the model. The field characteristic
is the set of admissible values of the parameters of the model. The field characteristic 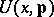 as a function of the variable
as a function of the variable  , with
, with 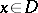 where
where 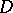 is the domain of observation, and of the parameter
is the domain of observation, and of the parameter 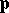 of the model, which is the quantity experimentally determined, can be computed with the aid of the known algorithm of the direct problem:
of the model, which is the quantity experimentally determined, can be computed with the aid of the known algorithm of the direct problem:
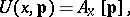 |
where 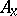 is, in general, a non-linear operator, depending on
is, in general, a non-linear operator, depending on  as a parameter. If
as a parameter. If 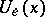 is an experimentally-determined field characteristic, the solution of the inverse problem will be
is an experimentally-determined field characteristic, the solution of the inverse problem will be 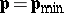 at which the minimum deviation of
at which the minimum deviation of 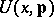 from
from 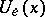 is realized, i.e.
is realized, i.e.
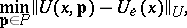 |
where 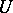 is the space of field characteristics. The mean-square norm is usually taken [6].
is the space of field characteristics. The mean-square norm is usually taken [6].
Two simple types of structural models of the medium that are used in geophysical investigations are: a half-space with local inhomogeneities, which is used in the analysis of the results furnished by geophysical prospecting conducted with the purpose of finding inhomogeneities in the Earth's crust, and a layered half-space in which the parameters of the medium vary with depth, which is used in solving stratification problems in geophysics.
The subsequent development of mathematical models consisted in refining the above two types of models for the sake of a more complete description of practical situations. For instance, local inhomogeneities in the layered half-space, a layered medium with a variable thickness of layers, etc., are studied. Even solutions of direct problems involving such complex structural models are only possible with the aid of computers. Finite-difference methods, finite-element methods, methods of integral equations, and projection methods are extensively used for this purpose.
The development of effective algorithms for the solution of direct problems in geophysics rendered the interpretation of quantitative experimental results more accurate. A large series of computations of direct problems for various families of mathematical models was carried out. These served for the compilation of albums of graphs of field characteristics, with the aid of which the inverse problems are solved by trial-and-error [7]. There has been intensive development of systems of automatic processing and interpretation of experimental data by the use of computers, [8]–[9].
References
| [1] | V.V. Fedynskii, "Geophysical exploration" , Moscow (1964) (In Russian) |
| [2] | A.K. Malovichko, "Methods of analytic continuation of anomaly of an attraction force and their applications to problems of gravity" , Moscow (1956) (In Russian) |
| [3] | V.I. Dmitriev, "Electromagnetic fields in non-homegeneous media" , Moscow (1969) (In Russian) |
| [4] | , Questions of the dynamic theory of propagation of seismic waves , 3 , Leningrad (1959) (In Russian) |
| [5] | A.N. Tikhonov, "Regularization of incorrectly posed problems" Soviet Math. Dokl. , 4 : 6 (1963) pp. 1624–1627 Dokl. Akad. Nauk SSSR , 153 : 1 (1963) pp. 49–52 |
| [6] | M.M. [M.A. Lavrent'ev] Lavrentiev, "Some improperly posed problems of mathematical physics" , Springer (1967) (Translated from Russian) |
| [7] | A.N. Tikhonov, "On the stability of inverse problems" Dokl. Akad. Nauk SSSR , 39 : 5 (1943) pp. 176–179 |
| [8] | A.N. Tikhonov, V.I. [V.I. Arsenin] Arsenine, "Solutions of ill-posed problems" , Halted Press (1977) (Translated from Russian) |
| [9] | A.N. Tikhonov (ed.) A.V. Goncharskii (ed.) , Ill-posed problems in the natural sciences , Moscow (1987) (In Russian) |
Comments
In [a1] there is an overview of Russian contributions to ill-posed problems, including Tikhonov's regularization method. [a2] deals with computational methods for inverse problems in geophysics. The powerful inverse scattering method also found its way in seismology, see [a3].
References
| [a1] | V.A. Morozov, "Methods for solving incorrectly posed problems" , Springer (1984) (Translated from Russian) |
| [a2] | A. Tarantola, "Inverse problem theory. Methods for data fitting and model parameter estimation" , Elsevier (1987) |
| [a3] | A.B. Weglein, "The inverse scattering concept and its seismic application" A.A. Fitch (ed.) , Developments in geophysical exploration , 6 , Elsevier (1985) pp. 111–138 |
| [a4] | K. Aki, P.G. Richards, "Quantitative seismology" , I–II , Freeman (1980) |
| [a5] | J.D. Achenbach, "Wave propagation in elastic solids" , North-Holland (1973) |
| [a6] | J.H.M.T. van der Hyden, "Propagation of transient elastic waves in stratified anisotropic media" , North-Holland (1987) |
Geophysics, mathematical problems in. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Geophysics,_mathematical_problems_in&oldid=18575