Geometric ring
A local ring of an algebraic variety or a completion of such a ring. A commutative ring obtained from a ring of polynomials over a field by means of the operations of completion, localization and factorization by a prime ideal is called an algebro-geometric ring [3]. A local ring of an irreducible algebraic variety does not obtain nilpotent elements as a result of completion [2]. This property of a local ring is known as analytic reducibility. A similar fact concerning local rings of normal varieties [1] is that the completion of a local ring of a normal algebraic variety is a normal ring (analytic normality). Examples of local Noetherian rings that are not analytically reduced or analytically normal are known [4]. A pseudo-geometric ring is a Noetherian ring any quotient ring of which by a prime ideal is a Japanese ring. An integral domain 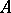 is called a Japanese ring if its integral closure in a finite extension of the field of fractions is a finite
is called a Japanese ring if its integral closure in a finite extension of the field of fractions is a finite 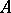 -module [5]. The class of pseudo-geometric rings is closed with respect to localizations and extensions of finite type; it includes the ring of integers and all complete local rings. See also Excellent ring.
-module [5]. The class of pseudo-geometric rings is closed with respect to localizations and extensions of finite type; it includes the ring of integers and all complete local rings. See also Excellent ring.
References
| [1] | O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975) |
| [2] | C. Chevalley, "Intersection of algebraic and algebroid varieties" Trans. Amer. Math. Soc. , 57 (1945) pp. 1–85 |
| [3] | P. Samuel, "Algèbre locale" , Gauthier-Villars (1953) |
| [4] | M. Nagata, "Local rings" , Interscience (1962) |
| [5] | A. Grothendieck, "Eléments de géometrie algébrique IV. Etude locale des schémas et des morphismes des schémas" Publ. Math. IHES : 32 (1967) |
Geometric ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Geometric_ring&oldid=16165