Geodesic torsion
of a curve 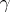 on a surface
on a surface 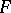 in
in 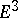
The rate of rotation of the tangent plane to 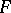 around the tangent to
around the tangent to 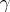 . The rate is measured with respect to the arc length
. The rate is measured with respect to the arc length  during the movement of the tangent lines along
during the movement of the tangent lines along 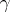 . The curve
. The curve 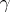 and the surface
and the surface 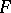 are supposed to be regular and oriented. The geodesic torsion on
are supposed to be regular and oriented. The geodesic torsion on 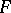 is determined by the points and the direction of the curve and equals the torsion of the geodesic line in that direction. The geodesic torsion is given by
is determined by the points and the direction of the curve and equals the torsion of the geodesic line in that direction. The geodesic torsion is given by
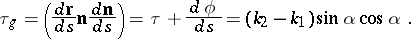 |
Here  is the radius vector of the curve;
is the radius vector of the curve; 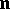 is the unit normal to
is the unit normal to 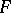 ;
;  is the ordinary torsion of
is the ordinary torsion of 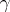 ; and
; and 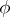 is the angle between the osculating plane of the curve and the tangent plane to the surface;
is the angle between the osculating plane of the curve and the tangent plane to the surface; 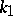 and
and 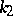 are the principal curvatures of the surface and
are the principal curvatures of the surface and 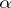 is the angle between the curve and the direction of
is the angle between the curve and the direction of 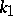 .
.
Comments
References
| [a1] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) pp. 395 (Translated from French) |
| [a2] | M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) pp. 153; 261 |
| [a3] | M. Spivak, "A comprehensive introduction to differential geometry" , 3 , Publish or Perish pp. 1–5 |
Geodesic torsion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Geodesic_torsion&oldid=18383