Geodesic line
geodesic
A geometric concept which is a generalization of the concept of a straight line (or a segment of a straight line) in Euclidean geometry to spaces of a more general type. The definitions of geodesic lines in various spaces depend on the particular structure (metric, line element, linear connection) on which the geometry of the particular space is based. In the geometry of spaces in which the metric is considered to be specified in advance, geodesic lines are defined as locally shortest. In spaces with a connection a geodesic line is defined as a curve for which the tangent vector field is parallel along this curve. In Riemannian and Finsler geometries, where the line element is given in advance (in other words, a metric in the tangent space at each point of the considered manifold is given), while the lengths of lines are obtained by subsequent integration, geodesic lines are defined as extremals of the length functional.
Geodesic lines were first studied by J. Bernoulli and L. Euler, who attempted to find the shortest lines on regular surfaces in Euclidean space. On such lines the geodesic curvature vanishes, and the principal normal of such curves is parallel to the normal to the surface. Geodesic lines are preserved under isometric deformation. The motion of a conservative mechanical system with a finite number of degrees of freedom is described by a geodesic line in a suitably-chosen Riemannian space.
Geodesic lines in Riemannian spaces have been studied most thoroughly. Let 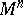 be an
be an  -dimensional Riemannian space with metric tensor
-dimensional Riemannian space with metric tensor 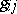 of class
of class 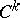 ,
, 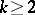 . The definition of a geodesic line as an extremal makes it possible to write down its differential equation in arbitrary local coordinates
. The definition of a geodesic line as an extremal makes it possible to write down its differential equation in arbitrary local coordinates 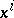 ,
, 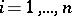 , for any parametrization
, for any parametrization 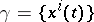 :
:
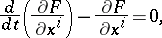 |
where
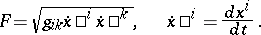 |
Another, equivalent, form of the equations of geodesic lines is derived from the postulate of parallelity of the tangent vector 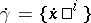 along
along 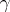 . If
. If 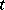 is the arc length
is the arc length  along a geodesic, or a linear function of
along a geodesic, or a linear function of  , then
, then
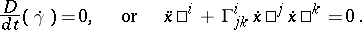 | (1) |
The definition of a geodesic line by equation (1) also involves a canonical selection of a parameter. In such a definition a geodesic line  , with initial tangent vector
, with initial tangent vector 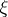 ,
, 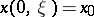 ,
, 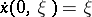 , passes through a given point
, passes through a given point 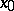 . The mapping
. The mapping 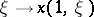 of the tangent space at
of the tangent space at 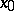 into the space under consideration is the exponential mapping with pole
into the space under consideration is the exponential mapping with pole 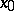 . Near the pole
. Near the pole 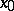 it is a diffeomorphism, which introduces Riemannian coordinates into the space under consideration.
it is a diffeomorphism, which introduces Riemannian coordinates into the space under consideration.
A number of properties of geodesic lines are preserved for curves represented by second-order equations 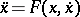 if, like in (1), the function
if, like in (1), the function 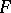 is a homogeneous function of the second degree in
is a homogeneous function of the second degree in 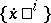 . The search for such equations in terms of tangent bundles yields the concepts of a spray and their integral curves. Geodesic lines are a special case of such curves [2].
. The search for such equations in terms of tangent bundles yields the concepts of a spray and their integral curves. Geodesic lines are a special case of such curves [2].
The local behaviour of geodesic curves is similar to that of straight lines in Euclidean space. A sufficiently short arc of a geodesic line is the shortest among all rectifiable curves with the same ends. Only one geodesic line passes through any point in a given direction. Each point has a neighbourhood 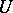 in which any two points can be connected by a unique geodesic line lying in
in which any two points can be connected by a unique geodesic line lying in 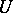 [3].
[3].
The question of the distance to which an arc of a geodesic line issuing from a point 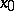 may be extended so that it remains the shortest among all curves in a neighbourhood of
may be extended so that it remains the shortest among all curves in a neighbourhood of 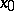 is one of the problems of the calculus of variations. A comparison of a geodesic line with nearby curves is based on the study of the second variation of the length by considering particular fields of velocities (the Jacobi vector field) along the geodesic line
is one of the problems of the calculus of variations. A comparison of a geodesic line with nearby curves is based on the study of the second variation of the length by considering particular fields of velocities (the Jacobi vector field) along the geodesic line 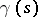 belonging to particular variations
belonging to particular variations 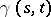 . For any fixed
. For any fixed 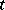 the curve
the curve 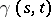 remains a geodesic, while the parameter
remains a geodesic, while the parameter  on it remains canonical. If at the origin of
on it remains canonical. If at the origin of 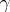 the velocity is zero, then the points on
the velocity is zero, then the points on 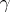 where some non-zero Jacobi vector field is zero are called conjugate points. Geodesic lines remain the shortest of all nearby curves up to the first conjugate point. For a geodesic arc extended beyond the conjugate point there exists a shorter curve with the same ends, which may be arbitrary near. A Jacobi vector field
where some non-zero Jacobi vector field is zero are called conjugate points. Geodesic lines remain the shortest of all nearby curves up to the first conjugate point. For a geodesic arc extended beyond the conjugate point there exists a shorter curve with the same ends, which may be arbitrary near. A Jacobi vector field 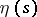 satisfies the equation
satisfies the equation
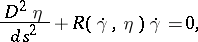 |
where  is a tangent vector to the geodesic
is a tangent vector to the geodesic 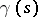 , while
, while 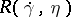 is the curvature transformation or, in Fermi coordinates
is the curvature transformation or, in Fermi coordinates  ,
, 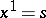 :
:
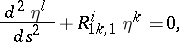 | (2) |
where 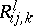 is the curvature tensor. The connection between the Jacobi vector field and the curvature determines the dependence of properties of the geodesics on the curvature of the space. For instance, in a space of negative curvature there are no conjugate points; if, in addition, the space is simply connected, then any geodesic arc is shortest, and geodesic lines issuing from a point diverge exponentially. These properties are of importance in the theory of dynamical systems (cf. Geodesic flow). The monotone nature of the effect of the curvature forms the subject of several so-called comparison theorems. In particular, the distance to the first conjugate point and the lengths of the vectors of the Jacobi vector field on this segment (normalized by the condition
is the curvature tensor. The connection between the Jacobi vector field and the curvature determines the dependence of properties of the geodesics on the curvature of the space. For instance, in a space of negative curvature there are no conjugate points; if, in addition, the space is simply connected, then any geodesic arc is shortest, and geodesic lines issuing from a point diverge exponentially. These properties are of importance in the theory of dynamical systems (cf. Geodesic flow). The monotone nature of the effect of the curvature forms the subject of several so-called comparison theorems. In particular, the distance to the first conjugate point and the lengths of the vectors of the Jacobi vector field on this segment (normalized by the condition 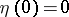 ,
, 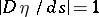 ) decrease as the curvature of the space increases. Here, under a comparison of two geodesic lines it is understood that all the curvatures of the second space majorize any curvature of the first space at points corresponding to the same lengths [4].
) decrease as the curvature of the space increases. Here, under a comparison of two geodesic lines it is understood that all the curvatures of the second space majorize any curvature of the first space at points corresponding to the same lengths [4].
In general relativity theory equation (2) is the source of physical interpretation of the space-time curvature by the behaviour of geodesic lines [5].
If the comparison is not restricted to nearby curves, the arc of a geodesic line may cease to be shortest before it has passed the conjugate point. This is possible even in a simply-connected space, i.e. the reasons for it may be both topological and metric.
The question of the effect of the curvature on the extension of the arc between conjugate points on which the geodesic line remains shortest is of importance in the study of the connection between the curvature and the topological structure of the space. The dependence of the number of closed geodesic lines or the number of different geodesic lines connecting two points on the topological structure of the space forms a subject of variational calculus in the large [6], [4], [7].
Families of geodesic lines, considered as possible trajectories of motion, form a subject of the theory of dynamical systems and ergodic theory.
In spaces with an affine connection geodesic lines are defined by equation (1). Local theorems on the existence and uniqueness of geodesic lines connecting two points, and on the existence of a convex neighbourhood, are preserved for such spaces.
Geodesic lines with similar properties are also defined in spaces with a projective connection, and also in cases of more general connections on manifolds.
The geometrization of the problems of variational calculus for functionals other than the length functional generated the concept of a Finsler space and the geodesic lines in that space. Separation of basic geometrical properties of such spaces led to the concept of geodesic geometry, defined by the presence and the extendability of geodesic lines.
The most intensively studied geodesic lines in metric spaces with an irregular metric are those on a convex surface and in a two-dimensional manifold of bounded curvature. Here, a geodesic line is not necessarily a smooth curve; it need have no extension or — in a two-dimensional manifold of bounded curvature — it may have a non-unique extension. A geodesic line on a convex surface invariably has a semi-tangent; if it can be extended, the extension is unique; geodesic lines issue from a point in almost-all directions. It was found that in such spaces the class of quasi-geodesic lines (cf. Quasi-geodesic line), which is the closure of the class of geodesic lines, is more natural than the class of geodesic lines itself [8].
References
| [1] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [2] | S. Lang, "Introduction to differentiable manifolds" , Interscience (1967) pp. App. III |
| [3] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1962) |
| [4] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) |
| [5] | J.L. Synge, "Relativity: the general theory" , North-Holland & Interscience (1960) |
| [6] | L.A. Lyusternik, L.G. [L.G. Shnirel'man] Schnirelmann, "Méthode topologiques dans les problèmes variationelles" , Hermann (1934) (Translated from Russian) |
| [7] | J.W. Milnor, "Morse theory" , Princeton Univ. Press (1963) |
| [8] | A.D. Aleksandrov, "Die innere Geometrie der konvexen Flächen" , Akademie Verlag (1955) (Translated from Russian) |
Comments
Riemannian coordinates are usually called normal coordinates or geodesic polar coordinates, cf. Geodesic coordinates.
A convex neighbourhood, also called a normal neighbourhood, is a neighbourhood 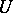 in which any two points can be connected by a unique geodesic in
in which any two points can be connected by a unique geodesic in 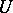 .
.
References
| [a1] | W. Klingenberg, "Lectures on closed geodesics" , Springer (1978) |
| [a2] | H. Busemann, "The geometry of geodesics" , Acad. Press (1955) |
| [a3] | W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) (Translated from German) |
| [a4] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
| [a5] | B. O'Neill, "Semi-Riemannian geometry (with applications to relativity)" , Acad. Press (1983) |
Geodesic line. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Geodesic_line&oldid=15374