Geodesic flow
A flow 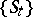 whose phase space is the manifold
whose phase space is the manifold  of vectors tangent to a Riemannian (more generally, a Finsler) manifold
of vectors tangent to a Riemannian (more generally, a Finsler) manifold  (the so-called configuration manifold of the flow), while the motion is defined as follows. Let
(the so-called configuration manifold of the flow), while the motion is defined as follows. Let  be a vector tangent to
be a vector tangent to 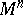 at a point
at a point  and let its length be
and let its length be 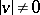 . Let a geodesic line
. Let a geodesic line  on
on 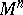 be drawn through
be drawn through  in the direction
in the direction  and let
and let 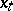 be the point on
be the point on 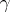 the distance of which from
the distance of which from  along
along 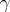 is
is 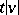 (where that direction on
(where that direction on 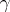 is considered to be positive which is identical with the direction of the vector
is considered to be positive which is identical with the direction of the vector  at
at  ). One then has
). One then has 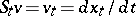 . In case
. In case  , one has
, one has 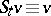 . It turns out that
. It turns out that 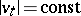 , and for this reason the vectors of unit length form a submanifold
, and for this reason the vectors of unit length form a submanifold 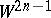 in
in 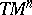 that is invariant with respect to
that is invariant with respect to 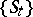 . A geodesic flow is often understood to mean the restriction of the flow
. A geodesic flow is often understood to mean the restriction of the flow 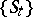 to
to 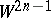 . In local coordinates a geodesic flow is described by a system of ordinary second-order differential equations, which, in the Riemannian case, have the form
. In local coordinates a geodesic flow is described by a system of ordinary second-order differential equations, which, in the Riemannian case, have the form
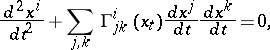 |
where 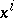 is the
is the 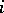 -th coordinate of the point
-th coordinate of the point  and the
and the 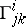 are the Christoffel symbols (cf. Christoffel symbol) of the second kind. A geodesic flow preserves the natural symplectic structure on
are the Christoffel symbols (cf. Christoffel symbol) of the second kind. A geodesic flow preserves the natural symplectic structure on 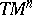 , while its restriction to
, while its restriction to 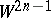 preserves the corresponding contact structure. Geodesic flows obviously play an important role in geometry (see also Variational calculus in the large). If, in addition, a certain change of time is made, then it is possible to reduce the description of the motion of a mechanical system, in accordance with the Maupertuis principle, to a geodesic flow.
preserves the corresponding contact structure. Geodesic flows obviously play an important role in geometry (see also Variational calculus in the large). If, in addition, a certain change of time is made, then it is possible to reduce the description of the motion of a mechanical system, in accordance with the Maupertuis principle, to a geodesic flow.
Comments
For the application to mechanical systems, see, for example, Section 45D and Appendices 1J and 4F in [a2]. The geodesic flows on (compact) manifolds of negative curvature have interesting dynamical properties (cf. Hyperbolic set; 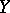 -system). See [a1]. For applications of geodesic flows in differential geometry, see [a3], Chapt. 3.
-system). See [a1]. For applications of geodesic flows in differential geometry, see [a3], Chapt. 3.
References
| [a1] | D.V. Anosov, "Geodesic flows on compact Riemannian manifolds of negative curvature" Proc. Steklov Inst. Math. , 90 (1969) Trudy Mat. Inst. Steklov. , 90 (1969) |
| [a2] | V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) |
| [a3] | W. Klingenberg, "Riemannian geometry" , Springer (1982) (Translated from German) |
Geodesic flow. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Geodesic_flow&oldid=18978