Generalized sequence

net

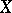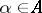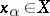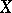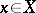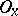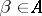A mapping of a directed set into a (topological) space , i.e. a correspondence according to which each is associated with some . A generalized sequence in a topological space is convergent in (sometimes one adds: with respect to the directed order ) to a point if for every neighbourhood of there exists a such that 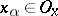for 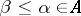. This is the concept of Moore–Smith convergence [3] (which seems more in conformity with intuitive ideas than convergence based on the concept of a filter). In terms of generalized sequences one can characterize the separation axioms (cf. Separation axiom), various types of compactness properties, as well as various constructions such as compactification, etc.

Ordinary sequences constitute a special case of generalized sequences, in which 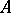is the set of natural numbers.

References

[1]	J.L. Kelley, "General topology" , v. Nostrand (1955)
[2]	M. Reed, B. Simon, "Methods of modern mathematical physics" , 1. Functional analysis , Acad. Press (1972)
[3]	E.H. Moore, H.L. Smith, "A general theory of limits" Amer. J. Math. , 44 (1922) pp. 102–121

Comments

The phrase "generalized sequence" is hardly ever used in the West; the commonly used terminology being "net" . See also Net (directed set). It should be noted that nets are necessary in the sense that sequences do not always suffice to characterize the various topological properties listed above.