Generalized function, derivative of a
A weak extension of the operation of ordinary differentiation. Let  be a generalized function,
be a generalized function,  . The generalized (weak) derivative
. The generalized (weak) derivative
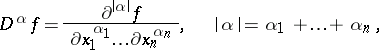 |
of order  is defined by the equation
is defined by the equation
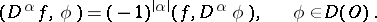 | (*) |
Since the operation  is linear and continuous from
is linear and continuous from  into
into  , the functional
, the functional  defined by the right-hand side of (*) is a generalized function in
defined by the right-hand side of (*) is a generalized function in 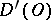 . If
. If 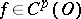 , then
, then 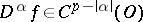 for all
for all 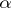 with
with 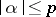 .
.
The following properties hold for the derivatives of a generalized function: the operation  is linear and continuous from
is linear and continuous from  into
into 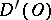 ; any generalized function in
; any generalized function in 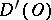 is infinitely differentiable (in the generalized sense); the result of differentiation does not depend on the order; the Leibniz formula is valid for the differentiation of a product
is infinitely differentiable (in the generalized sense); the result of differentiation does not depend on the order; the Leibniz formula is valid for the differentiation of a product 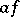 , when
, when  ; and
; and 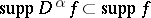 .
.
Let  . It may happen that a certain generalized derivative can be identified with some
. It may happen that a certain generalized derivative can be identified with some 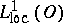 -function. In this case
-function. In this case 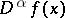 is a generalized derivative of function type.
is a generalized derivative of function type.
Examples.
1)  , where
, where 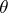 is the Heaviside function and
is the Heaviside function and 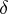 is the Dirac function (cf. Delta-function for both).
is the Dirac function (cf. Delta-function for both).
2) The general solution of the equation  in the class
in the class 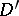 is an arbitrary constant.
is an arbitrary constant.
3) The trigonometric series
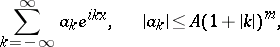 |
converges in  and it can be differentiated term-by-term in
and it can be differentiated term-by-term in  infinitely many times.
infinitely many times.
References
| [1] | L. Schwartz, "Théorie des distributions" , 1 , Hermann (1950) |
| [2] | S.L. Sobolev, "Applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian) |
Comments
References
| [a1] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5 |
| [a2] | L.V. Hörmander, "The analysis of linear partial differential operators" , 1 , Springer (1983) |
Generalized function, derivative of a. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Generalized_function,_derivative_of_a&oldid=17641