Difference between revisions of "Generalized derivative"
m |
|||
| Line 11: | Line 11: | ||
\end{equation} | \end{equation} | ||
| − | Another equivalent definition of the generalized derivative $\frac{\partial f}{\partial x_j}$ is the following. If | + | Another equivalent definition of the generalized derivative $\frac{\partial f}{\partial x_j}$ is the following. If $f$ can be modified on a set of $n$-dimensional measure zero so that the modified function (which will again be denoted by $f$) is locally [[Absolutely_continuous_function#Absolute_continuity_of_a_function|absolutely continuous]] with respect to $x_j$ for almost-all (in the sense of the $(n-1)$-dimensional Lebesgue measure) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379021.png" /> belonging to the projection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379022.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379023.png" /> onto the plane <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379024.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379025.png" /> has partial derivative (in the usual sense of the word) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379026.png" /> [[Almost-everywhere|almost-everywhere]] on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379027.png" />. If a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379028.png" /> almost-everywhere on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379029.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379030.png" /> is a generalized derivative of <img align="absmi |
ddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379031.png" /> with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379032.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379033.png" />. Thus, a generalized derivative is defined almost-everywhere on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379034.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379035.png" /> is continuous and the ordinary derivative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379036.png" /> is continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379037.png" />, then it is also a generalized derivative of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379038.png" /> with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379039.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379040.png" />. | ddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379031.png" /> with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379032.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379033.png" />. Thus, a generalized derivative is defined almost-everywhere on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379034.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379035.png" /> is continuous and the ordinary derivative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379036.png" /> is continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379037.png" />, then it is also a generalized derivative of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379038.png" /> with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379039.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043790/g04379040.png" />. | ||
Revision as of 14:26, 21 November 2012
of function type
An extension of the idea of a derivative to some classes of non-differentiable functions. The first definition is due to S.L. Sobolev (see [1], [2]), who arrived at a definition of a generalized derivative from the point of view of his concept of a generalized function.
Let $f$ and $\phi$ be locally integrable functions on an open set $\Omega\subset \mathbb R^n$, that is, Lebesgue integrable on any closed bounded set $F\subset\Omega$. Then $\phi$ is the generalized derivative of $f$ with respect to $x_j$ on $\Omega$, and one writes $\phi = \frac{\partial f}{\partial x_j}$, if for any infinitely-differentiable function $\psi$ with compact support in $\Omega$ (see Function of compact support)
\begin{equation}\label{eq:1} \int\limits_{\Omega}f(x)\frac{\partial \psi}{\partial x_j}(x)\,dx = -\int\limits_{\Omega}\phi(x) \psi(x)\,dx. \end{equation}
Another equivalent definition of the generalized derivative $\frac{\partial f}{\partial x_j}$ is the following. If $f$ can be modified on a set of $n$-dimensional measure zero so that the modified function (which will again be denoted by $f$) is locally absolutely continuous with respect to $x_j$ for almost-all (in the sense of the $(n-1)$-dimensional Lebesgue measure) 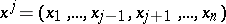 belonging to the projection
belonging to the projection 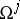 of
of  onto the plane
onto the plane 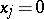 , then
, then 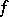 has partial derivative (in the usual sense of the word)
has partial derivative (in the usual sense of the word) 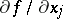 almost-everywhere on
almost-everywhere on  . If a function
. If a function 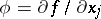 almost-everywhere on
almost-everywhere on  , then
, then 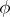 is a generalized derivative of
is a generalized derivative of 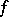 with respect to
with respect to 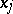 on
on  . Thus, a generalized derivative is defined almost-everywhere on
. Thus, a generalized derivative is defined almost-everywhere on  ; if
; if 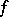 is continuous and the ordinary derivative
is continuous and the ordinary derivative  is continuous on
is continuous on  , then it is also a generalized derivative of
, then it is also a generalized derivative of 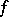 with respect to
with respect to 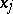 on
on  .
.
Generalized derivatives 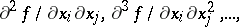 of a higher order are defined by induction. They are independent (almost-everywhere) of the order of differentiation.
of a higher order are defined by induction. They are independent (almost-everywhere) of the order of differentiation.
There is a third equivalent definition of a generalized derivative. Suppose that for each closed bounded set 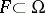 , the functions
, the functions 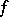 and
and 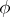 , defined on
, defined on  , have the properties:
, have the properties:
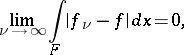 |
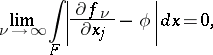 |
and suppose that the functions 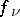 ,
, 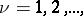 and their partial derivatives
and their partial derivatives 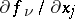 are continuous on
are continuous on  . Then
. Then  is the generalized partial derivative of
is the generalized partial derivative of 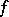 with respect to
with respect to 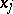 on
on  (
(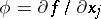 ) (see also Sobolev space).
) (see also Sobolev space).
From the point of view of the theory of generalized functions, a generalized derivative can be defined as follows: Suppose one is given a function 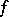 that is locally summable on
that is locally summable on  , considered as a generalized function, and let
, considered as a generalized function, and let 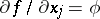 be the partial derivative in the sense of the theory of generalized functions. If
be the partial derivative in the sense of the theory of generalized functions. If 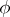 represents a function that is locally summable on
represents a function that is locally summable on  , then
, then 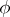 is a generalized derivative (in the first (original) sense).
is a generalized derivative (in the first (original) sense).
The concept of a generalized derivative had been considered even earlier (see [3] for example, where generalized derivatives with integrable square on  are considered). Subsequently, many investigators arrived at this concept independently of their predecessors (on this question see [4]).
are considered). Subsequently, many investigators arrived at this concept independently of their predecessors (on this question see [4]).
References
| [1] | S.L. Sobolev, "Le problème de Cauchy dans l'espace des fonctionnelles" Dokl. Akad. Nauk SSSR , 3 : 7 (1935) pp. 291–294 |
| [2] | S.L. Sobolev, "Méthode nouvelle à résoudre le problème de Cauchy pour les équations linéaires hyperboliques normales" Mat. Sb. , 1 (1936) pp. 39–72 |
| [3] | B. Levi, "Sul principio di Dirichlet" Rend. Circ. Mat. Palermo , 22 (1906) pp. 293–359 Zbl 37.0414.06 Zbl 37.0414.04 |
| [4] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) Zbl 0307.46024 |
Comments
References
| [a1] | S. Agmon, "Lectures on elliptic boundary value problems" , v. Nostrand (1965) MR0178246 Zbl 0142.37401 |
Generalized derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Generalized_derivative&oldid=28802