General linear group
The group of all  invertible matrices over an associative ring (cf. Associative rings and algebras)
invertible matrices over an associative ring (cf. Associative rings and algebras)  with a unit; the usual symbols are
with a unit; the usual symbols are  or
or  . The general linear group
. The general linear group  can also be defined as the automorphism group
can also be defined as the automorphism group  of the free right
of the free right  -module
-module  with
with  generators.
generators.
In research on the group 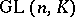 its normal structure is of considerable interest. The centre
its normal structure is of considerable interest. The centre 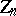 of the group
of the group  consists of scalar matrices with entries from the centre of the ring (cf. Centre of a ring)
consists of scalar matrices with entries from the centre of the ring (cf. Centre of a ring) 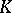 . When
. When 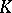 is commutative one defines the special linear group
is commutative one defines the special linear group 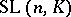 , which consists of matrices with determinant 1. When
, which consists of matrices with determinant 1. When 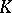 is a field, the commutator subgroup of the group
is a field, the commutator subgroup of the group 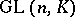 coincides with
coincides with 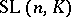 (apart from the case
(apart from the case 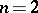 ,
,  ), and any normal subgroup of
), and any normal subgroup of  is either contained in
is either contained in 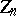 or contains
or contains  . In particular, the projective special linear group
. In particular, the projective special linear group
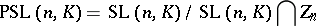 |
is a simple group (apart from the cases 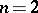 ,
, 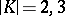 ).
).
If  is a skew-field and
is a skew-field and 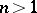 , any normal subgroup of
, any normal subgroup of 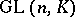 is either contained in
is either contained in 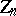 or contains the commutator subgroup
or contains the commutator subgroup 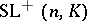 of
of 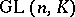 generated by transvections (cf. Transvection), and the quotient group
generated by transvections (cf. Transvection), and the quotient group  is simple. Also, there exists a natural isomorphism
is simple. Also, there exists a natural isomorphism
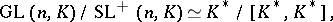 |
where 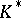 is the multiplicative group of the skew-field
is the multiplicative group of the skew-field 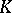 . If
. If 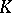 is finite-dimensional over its centre
is finite-dimensional over its centre 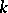 , then the role of
, then the role of  is played by the group of all matrices from
is played by the group of all matrices from 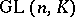 with reduced norm 1. The groups
with reduced norm 1. The groups  and
and 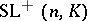 do not always coincide, although this is so if
do not always coincide, although this is so if 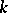 is a global field (see Kneser–Tits hypothesis).
is a global field (see Kneser–Tits hypothesis).
The study of the normal structure of general linear groups over a ring 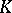 is associated with algebraic
is associated with algebraic 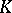 -theory. The group
-theory. The group 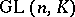 over a general ring
over a general ring 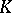 may contain numerous normal subgroups. For example, if
may contain numerous normal subgroups. For example, if 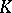 is a commutative ring without zero divisors and with a finite number of generators, then
is a commutative ring without zero divisors and with a finite number of generators, then 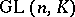 is a residually-finite group, i.e. for each element
is a residually-finite group, i.e. for each element 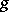 there exists a normal subgroup
there exists a normal subgroup 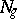 of finite index not containing
of finite index not containing 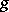 . In the case
. In the case 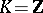 , the description of the normal subgroups of
, the description of the normal subgroups of 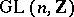 is in fact equivalent to the congruence problem for
is in fact equivalent to the congruence problem for 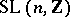 , since
, since
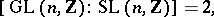 |
and any non-scalar normal subgroup of the group 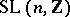 for
for 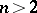 is a congruence subgroup.
is a congruence subgroup.
There is a deep analogy between the structure of general linear groups and that of other classical groups. This analogy extends also to simple algebraic groups and Lie groups.
References
| [1] | E. Artin, "Geometric algebra" , Interscience (1957) |
| [2] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) |
| [3] | H. Bass, "Algebraic 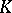 -theory" , Benjamin (1968) -theory" , Benjamin (1968) |
General linear group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=General_linear_group&oldid=13698