General integral
of a system of  ordinary differential equations
ordinary differential equations
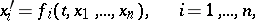 |
in a domain 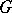
The set of  relations
relations
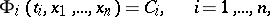 | (2) |
containing  parameters
parameters 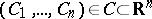 , and describing in implicit form the family of functions forming the general solution of this system in the domain
, and describing in implicit form the family of functions forming the general solution of this system in the domain 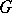 . Often the set of functions
. Often the set of functions
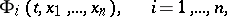 | (3) |
is called the general integral of , rather than the equations (2). Each of the equations (2) (or each function (3)) is called a first integral of . Sometimes a general integral of
means a more general set of equations than (2),
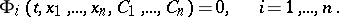 |
For an  -th order ordinary differential equation
-th order ordinary differential equation
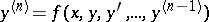 |
a general integral is a single relation with  parameters,
parameters,
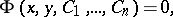 |
describing the general solution of this equation in the domain 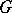 in the form of an implicit function.
in the form of an implicit function.
A general integral of a first-order partial differential equation is a relation between the variables in the equation involving one arbitrary function such that the equation is satisfied when the relation is substituted in it, for every choice of the arbitrary function.
See also Integral of a differential equation.
For references see General solution.
General integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=General_integral&oldid=15943