General-type algebraic surface

algebraic surface of general type

A surface of one of the broadest classes of algebraic surfaces (cf. Algebraic surface) in the Enriques classification. Namely, a smooth projective surface 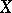over an algebraically closed field 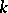is called an algebraic surface of general type if

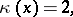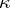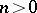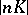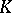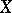where is the Kodaira dimension. This condition is equivalent to the fact that for an integer the linear system , where is the canonical divisor on , defines a birational mapping of onto its image in 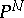for a certain 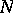. Every algebraic surface of general type possesses a birational morphism onto its minimal model.

Minimal algebraic surfaces of general type are characterized (see [1], [3], [6]) by each of the following sets of properties:

a) 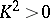and 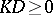for any effective divisor ;

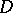b) 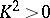and 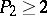, where 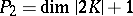is the second plurigenus of ;

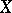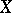c) and the surface is not rational (cf. Rational surface);

d) there exists an integer 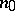such that, for any 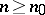, the mapping 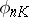defined by the system 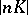is a birational morphism of 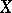onto its image in .

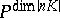For algebraic surfaces of general type, relations (in the form of inequalities) exist between the numerical characteristics. Let 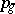be the geometric genus and let 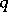be the irregularity of 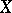. Then for a minimal algebraic surface of general type the following inequalities hold:

1) ;

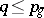2) 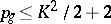if 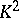is even, 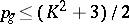if 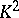is odd (these two inequalities are called Noether's inequalities);

3) 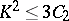, where 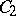is the second Chern class of 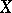(or the topological Euler characteristic).

The most complete result on multi-canonical mappings 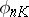of algebraic surfaces of general type is the Bombieri–Kodaira theorem: Let 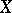be a minimal algebraic surface of general type over an algebraically closed field of characteristic 0, then the mapping

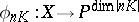is a birational morphism onto its own image for all 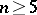. Algebraic surfaces of general type for which 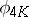does not possess this property exist (see [5], , [9]).

References

[1]	I.R., et al. Shafarevich, "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1967) Trudy Mat. Inst. Steklov. , 75 (1965)
[2]	F.A. Bogomolov, "Holomorphic tensors and vector bundles on projective varieties" Math. USSR-Izv. , 13 : 3 (1979) pp. 499–555 Izv. Akad. Nauk SSSR Ser. Mat. , 42 (1978) pp. 1227–1287
[3]	A. Beauville, "Surfaces algébriques complexes" Astérisque , 54 (1978)
[4]	E. Bombieri, "Canonical models of surfaces of general type" Publ. Math. IHES , 42 (1972) pp. 447–495
[5]	E. Bombieri, F. Catanese, "The tricanonical map of surfaces with 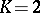, 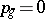" K.G. Ramanathan (ed.) , C.P. Ramanujam, a tribute , Springer (1978) pp. 279–290
[6]	D. Husemoller, "Classification and embeddings of surfaces" R. Hartshorne (ed.) , Algebraic geometry (Arcata, 1974) , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1974) pp. 329–420
[7]	E. Horikawa, "Algebraic surfaces of general type with small 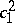, I" Ann. of Math. , 104 (1976) pp. 357–387
[8a]	E. Horikawa, "Algebraic surfaces of general type with small 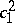, II" Invent. Math. , 37 (1976) pp. 121–155
[8b]	E. Horikawa, "Algebraic surfaces of general type with small 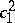, III" Invent. Math. , 47 (1978) pp. 209–248
[8c]	E. Horikawa, "Algebraic surfaces of general type with small 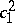, IV" Invent. Math. , 50 (1978–1979) pp. 103–128
[9]	K. Kodaira, "Pluricanonical systems on algebraic surfaces of general type" J. Math. Soc. Japan , 20 (1968) pp. 170–192
[10]	Y. Miyaoka, "On the Chern numbers of surfaces of general type" Invent. Math. , 42 (1977) pp. 225–237

Comments

Some of the above results have only been proved in characteristic zero; for instance, the inequality 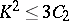only holds in characteristic zero.

For results on canonical models of surfaces of general type in positive characteristic see [a2].

References

[a1]	A. van de Ven, "Compact complex surfaces" , Springer (1984)
[a2]	T. Ekedahl, "Canonical models of surfaces of general type in positive characteristic" Publ. Math. IHES , 67 (1988) pp. 97–144