Difference between revisions of "General-type algebraic surface"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | g0437401.png | ||
| + | $#A+1 = 43 n = 6 | ||
| + | $#C+1 = 43 : ~/encyclopedia/old_files/data/G043/G.0403740 General\AAhtype algebraic surface, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''algebraic surface of general type'' | ''algebraic surface of general type'' | ||
| − | A surface of one of the broadest classes of algebraic surfaces (cf. [[Algebraic surface|Algebraic surface]]) in the Enriques classification. Namely, a smooth projective surface | + | A surface of one of the broadest classes of algebraic surfaces (cf. [[Algebraic surface|Algebraic surface]]) in the Enriques classification. Namely, a smooth projective surface $ X $ |
| + | over an algebraically closed field $ k $ | ||
| + | is called an algebraic surface of general type if | ||
| − | + | $$ | |
| + | \kappa ( x) = 2, | ||
| + | $$ | ||
| − | where | + | where $ \kappa $ |
| + | is the [[Kodaira dimension|Kodaira dimension]]. This condition is equivalent to the fact that for an integer $ n > 0 $ | ||
| + | the linear system $ | nK | $, | ||
| + | where $ K $ | ||
| + | is the [[canonical divisor]] on $ X $, | ||
| + | defines a birational mapping of $ X $ | ||
| + | onto its image in $ P ^ {N} $ | ||
| + | for a certain $ N $. | ||
| + | Every algebraic surface of general type possesses a birational morphism onto its minimal model. | ||
Minimal algebraic surfaces of general type are characterized (see [[#References|[1]]], [[#References|[3]]], [[#References|[6]]]) by each of the following sets of properties: | Minimal algebraic surfaces of general type are characterized (see [[#References|[1]]], [[#References|[3]]], [[#References|[6]]]) by each of the following sets of properties: | ||
| − | a) | + | a) $ K ^ { 2 } > 0 $ |
| + | and $ KD \geq 0 $ | ||
| + | for any effective divisor $ D $; | ||
| − | b) | + | b) $ K ^ { 2 } > 0 $ |
| + | and $ P _ {2} \geq 2 $, | ||
| + | where $ P _ {2} = \mathop{\rm dim} | 2 K | + 1 $ | ||
| + | is the second plurigenus of $ X $; | ||
| − | c) | + | c) $ K ^ { 2 } > 0 $ |
| + | and the surface $ X $ | ||
| + | is not rational (cf. [[Rational surface|Rational surface]]); | ||
| − | d) there exists an integer | + | d) there exists an integer $ n _ {0} $ |
| + | such that, for any $ n \geq n _ {0} $, | ||
| + | the mapping $ \phi _ {nK} $ | ||
| + | defined by the system $ | n K | $ | ||
| + | is a birational morphism of $ X $ | ||
| + | onto its image in $ P ^ { \mathop{\rm dim} | n K | } $. | ||
| − | For algebraic surfaces of general type, relations (in the form of inequalities) exist between the numerical characteristics. Let | + | For algebraic surfaces of general type, relations (in the form of inequalities) exist between the numerical characteristics. Let $ p _ {g} $ |
| + | be the [[Geometric genus|geometric genus]] and let $ q $ | ||
| + | be the [[Irregularity|irregularity]] of $ X $. | ||
| + | Then for a minimal algebraic surface of general type the following inequalities hold: | ||
| − | 1) | + | 1) $ q \leq p _ {g} $; |
| − | 2) | + | 2) $ p _ {g} \leq K ^ { 2 } /2 + 2 $ |
| + | if $ K ^ { 2 } $ | ||
| + | is even, $ p _ {g} \leq ( K ^ { 2 } + 3)/2 $ | ||
| + | if $ K ^ { 2 } $ | ||
| + | is odd (these two inequalities are called Noether's inequalities); | ||
| − | 3) | + | 3) $ K ^ { 2 } \leq 3C _ {2} $, |
| + | where $ C _ {2} $ | ||
| + | is the second [[Chern class|Chern class]] of $ X $( | ||
| + | or the topological [[Euler characteristic|Euler characteristic]]). | ||
| − | The most complete result on multi-canonical mappings | + | The most complete result on multi-canonical mappings $ \phi _ {nK} $ |
| + | of algebraic surfaces of general type is the Bombieri–Kodaira theorem: Let $ X $ | ||
| + | be a minimal algebraic surface of general type over an algebraically closed field of characteristic 0, then the mapping | ||
| − | + | $$ | |
| + | \phi _ {nK} : X \rightarrow P ^ { \mathop{\rm dim} | n K | } | ||
| + | $$ | ||
| − | is a birational morphism onto its own image for all | + | is a birational morphism onto its own image for all $ n \geq 5 $. |
| + | Algebraic surfaces of general type for which $ \phi _ {4K} $ | ||
| + | does not possess this property exist (see [[#References|[5]]], , [[#References|[9]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.R., et al. Shafarevich, "Algebraic surfaces" ''Proc. Steklov Inst. Math.'' , '''75''' (1967) ''Trudy Mat. Inst. Steklov.'' , '''75''' (1965) {{MR|1392959}} {{MR|1060325}} {{ZBL|0830.00008}} {{ZBL|0733.14015}} {{ZBL|0832.14026}} {{ZBL|0509.14036}} {{ZBL|0492.14024}} {{ZBL|0379.14006}} {{ZBL|0253.14006}} {{ZBL|0154.21001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> F.A. Bogomolov, "Holomorphic tensors and vector bundles on projective varieties" ''Math. USSR-Izv.'' , '''13''' : 3 (1979) pp. 499–555 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''42''' (1978) pp. 1227–1287 {{MR|}} {{ZBL|0439.14002}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A. Beauville, "Surfaces algébriques complexes" ''Astérisque'' , '''54''' (1978) {{MR|0485887}} {{ZBL|0394.14014}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E. Bombieri, "Canonical models of surfaces of general type" ''Publ. Math. IHES'' , '''42''' (1972) pp. 447–495 {{MR|0318163}} {{ZBL|0259.14005}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E. Bombieri, F. Catanese, "The tricanonical map of surfaces with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043740/g04374043.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043740/g04374044.png" />" K.G. Ramanathan (ed.) , ''C.P. Ramanujam, a tribute'' , Springer (1978) pp. 279–290 {{MR|541028}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> D. Husemoller, "Classification and embeddings of surfaces" R. Hartshorne (ed.) , ''Algebraic geometry (Arcata, 1974)'' , ''Proc. Symp. Pure Math.'' , '''29''' , Amer. Math. Soc. (1974) pp. 329–420 {{MR|0506292}} {{ZBL|0326.14009}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> E. Horikawa, "Algebraic surfaces of general type with small <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043740/g04374045.png" />, I" ''Ann. of Math.'' , '''104''' (1976) pp. 357–387</TD></TR><TR><TD valign="top">[8a]</TD> <TD valign="top"> E. Horikawa, "Algebraic surfaces of general type with small <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043740/g04374046.png" />, II" ''Invent. Math.'' , '''37''' (1976) pp. 121–155</TD></TR><TR><TD valign="top">[8b]</TD> <TD valign="top"> E. Horikawa, "Algebraic surfaces of general type with small <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043740/g04374047.png" />, III" ''Invent. Math.'' , '''47''' (1978) pp. 209–248 {{MR|501370}} {{ZBL|}} </TD></TR><TR><TD valign="top">[8c]</TD> <TD valign="top"> E. Horikawa, "Algebraic surfaces of general type with small <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043740/g04374048.png" />, IV" ''Invent. Math.'' , '''50''' (1978–1979) pp. 103–128</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> K. Kodaira, "Pluricanonical systems on algebraic surfaces of general type" ''J. Math. Soc. Japan'' , '''20''' (1968) pp. 170–192 {{MR|0224613}} {{ZBL|0157.27704}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> Y. Miyaoka, "On the Chern numbers of surfaces of general type" ''Invent. Math.'' , '''42''' (1977) pp. 225–237 {{MR|0460343}} {{ZBL|0374.14007}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.R., et al. Shafarevich, "Algebraic surfaces" ''Proc. Steklov Inst. Math.'' , '''75''' (1967) ''Trudy Mat. Inst. Steklov.'' , '''75''' (1965) {{MR|1392959}} {{MR|1060325}} {{ZBL|0830.00008}} {{ZBL|0733.14015}} {{ZBL|0832.14026}} {{ZBL|0509.14036}} {{ZBL|0492.14024}} {{ZBL|0379.14006}} {{ZBL|0253.14006}} {{ZBL|0154.21001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> F.A. Bogomolov, "Holomorphic tensors and vector bundles on projective varieties" ''Math. USSR-Izv.'' , '''13''' : 3 (1979) pp. 499–555 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''42''' (1978) pp. 1227–1287 {{MR|}} {{ZBL|0439.14002}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A. Beauville, "Surfaces algébriques complexes" ''Astérisque'' , '''54''' (1978) {{MR|0485887}} {{ZBL|0394.14014}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E. Bombieri, "Canonical models of surfaces of general type" ''Publ. Math. IHES'' , '''42''' (1972) pp. 447–495 {{MR|0318163}} {{ZBL|0259.14005}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E. Bombieri, F. Catanese, "The tricanonical map of surfaces with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043740/g04374043.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043740/g04374044.png" />" K.G. Ramanathan (ed.) , ''C.P. Ramanujam, a tribute'' , Springer (1978) pp. 279–290 {{MR|541028}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> D. Husemoller, "Classification and embeddings of surfaces" R. Hartshorne (ed.) , ''Algebraic geometry (Arcata, 1974)'' , ''Proc. Symp. Pure Math.'' , '''29''' , Amer. Math. Soc. (1974) pp. 329–420 {{MR|0506292}} {{ZBL|0326.14009}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> E. Horikawa, "Algebraic surfaces of general type with small <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043740/g04374045.png" />, I" ''Ann. of Math.'' , '''104''' (1976) pp. 357–387</TD></TR><TR><TD valign="top">[8a]</TD> <TD valign="top"> E. Horikawa, "Algebraic surfaces of general type with small <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043740/g04374046.png" />, II" ''Invent. Math.'' , '''37''' (1976) pp. 121–155</TD></TR><TR><TD valign="top">[8b]</TD> <TD valign="top"> E. Horikawa, "Algebraic surfaces of general type with small <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043740/g04374047.png" />, III" ''Invent. Math.'' , '''47''' (1978) pp. 209–248 {{MR|501370}} {{ZBL|}} </TD></TR><TR><TD valign="top">[8c]</TD> <TD valign="top"> E. Horikawa, "Algebraic surfaces of general type with small <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043740/g04374048.png" />, IV" ''Invent. Math.'' , '''50''' (1978–1979) pp. 103–128</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> K. Kodaira, "Pluricanonical systems on algebraic surfaces of general type" ''J. Math. Soc. Japan'' , '''20''' (1968) pp. 170–192 {{MR|0224613}} {{ZBL|0157.27704}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> Y. Miyaoka, "On the Chern numbers of surfaces of general type" ''Invent. Math.'' , '''42''' (1977) pp. 225–237 {{MR|0460343}} {{ZBL|0374.14007}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | Some of the above results have only been proved in characteristic zero; for instance, the inequality | + | Some of the above results have only been proved in characteristic zero; for instance, the inequality $ K ^ { 2 } \leq 3 C _ {2} $ |
| + | only holds in characteristic zero. | ||
For results on canonical models of surfaces of general type in positive characteristic see [[#References|[a2]]]. | For results on canonical models of surfaces of general type in positive characteristic see [[#References|[a2]]]. | ||
Latest revision as of 19:41, 5 June 2020
algebraic surface of general type
A surface of one of the broadest classes of algebraic surfaces (cf. Algebraic surface) in the Enriques classification. Namely, a smooth projective surface $ X $ over an algebraically closed field $ k $ is called an algebraic surface of general type if
$$ \kappa ( x) = 2, $$
where $ \kappa $ is the Kodaira dimension. This condition is equivalent to the fact that for an integer $ n > 0 $ the linear system $ | nK | $, where $ K $ is the canonical divisor on $ X $, defines a birational mapping of $ X $ onto its image in $ P ^ {N} $ for a certain $ N $. Every algebraic surface of general type possesses a birational morphism onto its minimal model.
Minimal algebraic surfaces of general type are characterized (see [1], [3], [6]) by each of the following sets of properties:
a) $ K ^ { 2 } > 0 $ and $ KD \geq 0 $ for any effective divisor $ D $;
b) $ K ^ { 2 } > 0 $ and $ P _ {2} \geq 2 $, where $ P _ {2} = \mathop{\rm dim} | 2 K | + 1 $ is the second plurigenus of $ X $;
c) $ K ^ { 2 } > 0 $ and the surface $ X $ is not rational (cf. Rational surface);
d) there exists an integer $ n _ {0} $ such that, for any $ n \geq n _ {0} $, the mapping $ \phi _ {nK} $ defined by the system $ | n K | $ is a birational morphism of $ X $ onto its image in $ P ^ { \mathop{\rm dim} | n K | } $.
For algebraic surfaces of general type, relations (in the form of inequalities) exist between the numerical characteristics. Let $ p _ {g} $ be the geometric genus and let $ q $ be the irregularity of $ X $. Then for a minimal algebraic surface of general type the following inequalities hold:
1) $ q \leq p _ {g} $;
2) $ p _ {g} \leq K ^ { 2 } /2 + 2 $ if $ K ^ { 2 } $ is even, $ p _ {g} \leq ( K ^ { 2 } + 3)/2 $ if $ K ^ { 2 } $ is odd (these two inequalities are called Noether's inequalities);
3) $ K ^ { 2 } \leq 3C _ {2} $, where $ C _ {2} $ is the second Chern class of $ X $( or the topological Euler characteristic).
The most complete result on multi-canonical mappings $ \phi _ {nK} $ of algebraic surfaces of general type is the Bombieri–Kodaira theorem: Let $ X $ be a minimal algebraic surface of general type over an algebraically closed field of characteristic 0, then the mapping
$$ \phi _ {nK} : X \rightarrow P ^ { \mathop{\rm dim} | n K | } $$
is a birational morphism onto its own image for all $ n \geq 5 $. Algebraic surfaces of general type for which $ \phi _ {4K} $ does not possess this property exist (see [5], , [9]).
References
| [1] | I.R., et al. Shafarevich, "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1967) Trudy Mat. Inst. Steklov. , 75 (1965) MR1392959 MR1060325 Zbl 0830.00008 Zbl 0733.14015 Zbl 0832.14026 Zbl 0509.14036 Zbl 0492.14024 Zbl 0379.14006 Zbl 0253.14006 Zbl 0154.21001 |
| [2] | F.A. Bogomolov, "Holomorphic tensors and vector bundles on projective varieties" Math. USSR-Izv. , 13 : 3 (1979) pp. 499–555 Izv. Akad. Nauk SSSR Ser. Mat. , 42 (1978) pp. 1227–1287 Zbl 0439.14002 |
| [3] | A. Beauville, "Surfaces algébriques complexes" Astérisque , 54 (1978) MR0485887 Zbl 0394.14014 |
| [4] | E. Bombieri, "Canonical models of surfaces of general type" Publ. Math. IHES , 42 (1972) pp. 447–495 MR0318163 Zbl 0259.14005 |
| [5] | E. Bombieri, F. Catanese, "The tricanonical map of surfaces with 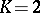 , , 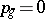 " K.G. Ramanathan (ed.) , C.P. Ramanujam, a tribute , Springer (1978) pp. 279–290 MR541028 " K.G. Ramanathan (ed.) , C.P. Ramanujam, a tribute , Springer (1978) pp. 279–290 MR541028 |
| [6] | D. Husemoller, "Classification and embeddings of surfaces" R. Hartshorne (ed.) , Algebraic geometry (Arcata, 1974) , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1974) pp. 329–420 MR0506292 Zbl 0326.14009 |
| [7] | E. Horikawa, "Algebraic surfaces of general type with small 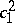 , I" Ann. of Math. , 104 (1976) pp. 357–387 , I" Ann. of Math. , 104 (1976) pp. 357–387 |
| [8a] | E. Horikawa, "Algebraic surfaces of general type with small 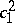 , II" Invent. Math. , 37 (1976) pp. 121–155 , II" Invent. Math. , 37 (1976) pp. 121–155 |
| [8b] | E. Horikawa, "Algebraic surfaces of general type with small 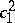 , III" Invent. Math. , 47 (1978) pp. 209–248 MR501370 , III" Invent. Math. , 47 (1978) pp. 209–248 MR501370 |
| [8c] | E. Horikawa, "Algebraic surfaces of general type with small 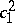 , IV" Invent. Math. , 50 (1978–1979) pp. 103–128 , IV" Invent. Math. , 50 (1978–1979) pp. 103–128 |
| [9] | K. Kodaira, "Pluricanonical systems on algebraic surfaces of general type" J. Math. Soc. Japan , 20 (1968) pp. 170–192 MR0224613 Zbl 0157.27704 |
| [10] | Y. Miyaoka, "On the Chern numbers of surfaces of general type" Invent. Math. , 42 (1977) pp. 225–237 MR0460343 Zbl 0374.14007 |
Comments
Some of the above results have only been proved in characteristic zero; for instance, the inequality $ K ^ { 2 } \leq 3 C _ {2} $ only holds in characteristic zero.
For results on canonical models of surfaces of general type in positive characteristic see [a2].
References
| [a1] | A. van de Ven, "Compact complex surfaces" , Springer (1984) Zbl 0718.14023 |
| [a2] | T. Ekedahl, "Canonical models of surfaces of general type in positive characteristic" Publ. Math. IHES , 67 (1988) pp. 97–144 MR0972344 Zbl 0674.14028 |
General-type algebraic surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=General-type_algebraic_surface&oldid=23840