Gaussian channel
A communication channel whose transition function determines a conditional Gaussian distribution. More precisely, a communication channel  is called a Gaussian channel on the finite interval
is called a Gaussian channel on the finite interval  if the following conditions hold: 1) the spaces of values of the input and output signals,
if the following conditions hold: 1) the spaces of values of the input and output signals,  and
and  , are spaces of real-valued functions
, are spaces of real-valued functions  and
and  ,
,  , with the usual
, with the usual  -algebras of measurable sets (that is, the input and output signals of a Gaussian channel are given by stochastic processes
-algebras of measurable sets (that is, the input and output signals of a Gaussian channel are given by stochastic processes  and
and  , respectively); 2) for any fixed
, respectively); 2) for any fixed 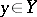 the transition function
the transition function 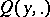 of the channel determines a conditional Gaussian distribution (one says that a collection of random variables has a conditional Gaussian distribution if every finite subfamily has a conditional finite-dimensional normal distribution with second moments that are independent of the conditioning); and 3) the restriction
of the channel determines a conditional Gaussian distribution (one says that a collection of random variables has a conditional Gaussian distribution if every finite subfamily has a conditional finite-dimensional normal distribution with second moments that are independent of the conditioning); and 3) the restriction 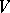 is imposed only on the second moment of the random variable
is imposed only on the second moment of the random variable  .
.
An example of a Gaussian channel on  is a channel whose input signal is given by a stationary random sequence
is a channel whose input signal is given by a stationary random sequence 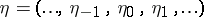 and whose output signal is the stationary random sequence
and whose output signal is the stationary random sequence 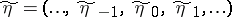 , obtained according to the formulas
, obtained according to the formulas
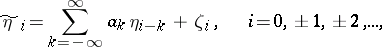 |
where 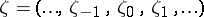 is a stationary Gaussian random sequence independent of
is a stationary Gaussian random sequence independent of 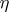 with
with 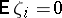 ,
,  and with spectral density
and with spectral density 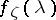 ,
, 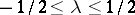 . The restriction on the input signal has the form
. The restriction on the input signal has the form
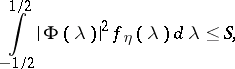 |
where  is the spectral density of
is the spectral density of 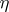 ,
, 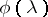 is some function and
is some function and  is a constant. The capacity of such a channel is given by the formula
is a constant. The capacity of such a channel is given by the formula
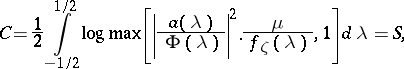 |
where 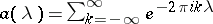 and
and 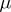 is determined by the equation
is determined by the equation
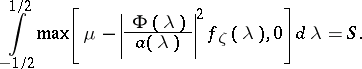 |
See also [1], ,
cited in Communication channel.
References
| [1] | J.M. Wozencraft, I.M. Jacobs, "Principles of communication engineering" , Wiley (1965) |
Gaussian channel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gaussian_channel&oldid=15220