Gauss quadrature formula
The quadrature formula
 |
in which the nodes (cf. Node)  and the weights
and the weights  are so selected that the formula is exact for the functions
are so selected that the formula is exact for the functions
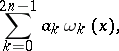 |
where  are given linearly independent functions (the integration limits may well be infinite). The formula was introduced by C.F. Gauss [1] for
are given linearly independent functions (the integration limits may well be infinite). The formula was introduced by C.F. Gauss [1] for 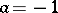 ,
,  ,
,  . He obtained the following formula, which is exact for an arbitrary polynomial of degree not exceeding
. He obtained the following formula, which is exact for an arbitrary polynomial of degree not exceeding  :
:
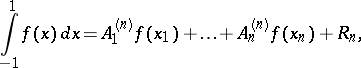 |
where the 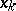 are the roots of the Legendre polynomial (cf. Legendre polynomials)
are the roots of the Legendre polynomial (cf. Legendre polynomials) 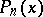 , while
, while  and
and  are defined by the formulas
are defined by the formulas
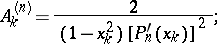 |
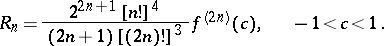 |
The formula is used whenever the integrand is sufficiently smooth, and the gain in the number of nodes is substantial; for instance, if  is determined from expensive experiments or during the computation of multiple integrals as repeated integrals. In such practical applications a suitable choice of the weight function and of the functions
is determined from expensive experiments or during the computation of multiple integrals as repeated integrals. In such practical applications a suitable choice of the weight function and of the functions  is very important.
is very important.
Tables of nodes in Gauss' quadrature formula are available for wide classes of 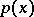 and
and 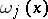 [5]; in particular for
[5]; in particular for 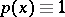 ,
,  up to
up to  .
.
If  ,
, 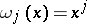 , Gauss' quadrature formula is employed in standard integration programs with an automatic step selection as a method of computing integrals by subdivision of subsegments [6].
, Gauss' quadrature formula is employed in standard integration programs with an automatic step selection as a method of computing integrals by subdivision of subsegments [6].
References
| [1] | C.F. Gauss, "Methodus nova integralium valores per approximationem inveniendi" , Werke , 3 , K. Gesellschaft Wissenschaft. Göttingen (1886) pp. 163–196 |
| [2] | N.M. Krylov, "Approximate calculation of integrals" , Macmillan (1962) (Translated from Russian) |
| [3] | V.I. Krylov, L.T. Shul'gina, "Handbook on numerical integration" , Moscow (1966) (In Russian) |
| [4] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
| [5] | A.H. Stroud, "Gaussian quadrature formulas" , Prentice-Hall (1966) |
| [6] | , A standard program for the computation of single integrals of quadratures of Gauss' type : 26 , Moscow (1967) (In Russian) |
Comments
A detailed investigation of the general Gauss formulas 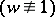 was carried out by E.B. Christoffel [a3] and the quadrature coefficients are therefore also called Christoffel coefficients or Christoffel numbers (see also [a1]). Tables of these coefficients may be found in [a2].
was carried out by E.B. Christoffel [a3] and the quadrature coefficients are therefore also called Christoffel coefficients or Christoffel numbers (see also [a1]). Tables of these coefficients may be found in [a2].
References
| [a1] | F.B. Hildebrand, "Introduction to numerical analysis" , McGraw-Hill (1974) |
| [a2] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , 25 , Dover, reprint (1970) |
| [a3] | E.B. Christoffel, "Ueber die Gausssche Quadratur und eine Verallgemeinerung derselben" J. Reine Angew. Math. , 55 (1858) pp. 81–82 |
| [a4] | P.J. Davis, P. Rabinowitz, "Methods of numerical integration" , Acad. Press (1984) |
| [a5] | R. Piessens, et al., "Quadpack" , Springer (1983) |
Gauss quadrature formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss_quadrature_formula&oldid=11718