Gauss number
A complex integer 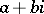 , where
, where  and
and 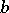 are arbitrary rational integers. Geometrically, the Gauss numbers form the lattice of all points with integral rational coordinates on the plane. Such numbers were first considered in 1832 by C.F. Gauss in his work on biquadratic residues. He also discovered the properties of the set
are arbitrary rational integers. Geometrically, the Gauss numbers form the lattice of all points with integral rational coordinates on the plane. Such numbers were first considered in 1832 by C.F. Gauss in his work on biquadratic residues. He also discovered the properties of the set 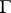 of complex integers.
of complex integers.
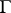 is a domain; its units (i.e. divisors of the unit element) are
is a domain; its units (i.e. divisors of the unit element) are  , and there are no other units. One kind of primes (i.e. numbers that cannot be decomposed into a non-trivial product) of
, and there are no other units. One kind of primes (i.e. numbers that cannot be decomposed into a non-trivial product) of 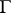 (the Gaussian primes) are the numbers of the form
(the Gaussian primes) are the numbers of the form
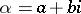 |
the norms (moduli) 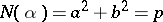 of which are rational prime numbers
of which are rational prime numbers 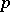 of the form
of the form 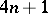 or
or 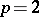 ; the other kind are rational prime numbers of the form
; the other kind are rational prime numbers of the form 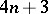 . Examples of Gaussian primes are
. Examples of Gaussian primes are 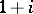 ,
, 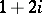 ,
,  ,
,  ,
, 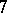 , etc.
, etc.
Any number in  can be uniquely decomposed into a product of primes in
can be uniquely decomposed into a product of primes in 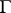 , up to units and ordering. Domains with this property are called unique factorization domains or Gaussian rings (cf. also Factorial ring).
, up to units and ordering. Domains with this property are called unique factorization domains or Gaussian rings (cf. also Factorial ring).
In the theory of biquadratic residues the Gaussian numbers were the first simple and important instance of an extension of the field of rational numbers.
References
| [1] | C.F. Gauss, "Disquisitiones Arithmeticae" , Yale Univ. Press (1966) (Translated from Latin) |
Comments
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Clarendon Press (1960) pp. Chapt. XV |
Gauss number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss_number&oldid=15950