Gauss-Laplace distribution
One of the names given to the normal distribution which, together with other names such as Gauss law, Gaussian distribution, second law of Laplace, Laplace–Gauss distribution, etc., connects the discovery and the first applications of this distribution to various problems in probability theory with the names of C.F. Gauss and P. Laplace. Gauss (1809) and Laplace (1812) introduced the normal distribution in connection with their studies on the theory of errors and method of least squares (cf. Errors, theory of; Least squares, method of). Thus, in the theory of (observational) errors, developed by Gauss for problems in astronomy and theoretical geodesy, the probability density of random errors is given by the expression
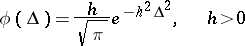 |
(cf. Gauss law). In addition, Laplace obtained the integral (the Laplace function)
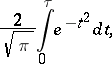 |
which gives the approximate value (for large  ) of the probability that the number of successful outcomes in
) of the probability that the number of successful outcomes in  Bernoulli trials with a probability of success
Bernoulli trials with a probability of success 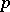 lies in between
lies in between 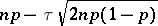 and
and 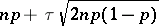 (the so-called limit formula of Laplace). At an earlier date (1733), the relation in which the normal distribution appears as the limit form of the binomial distribution (with
(the so-called limit formula of Laplace). At an earlier date (1733), the relation in which the normal distribution appears as the limit form of the binomial distribution (with 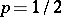 ) had been discovered by A. de Moivre.
) had been discovered by A. de Moivre.
References
| [1] | C.F. Gauss, "Theoria motus corporum coellestium" , Werke , 7 , K. Gesellschaft Wissenschaft. Göttingen (1809) (English translation: C.H. Davis (ed.), Dover, 1963) |
| [2] | P.S. Laplace, "Théorie analytique des probabilités" , Paris (1812) |
| [3] | I. Todhunter, "A history of the mathematical theory of probability" , Chelsea, reprint (1949) |
Gauss-Laplace distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss-Laplace_distribution&oldid=13322