Galois theory, inverse problem of
The problem of constructing a finite normal extension of a given field  with given Galois group (cf. Galois theory), and of stating the conditions which ensure the existence (and non-existence) of such an extension over
with given Galois group (cf. Galois theory), and of stating the conditions which ensure the existence (and non-existence) of such an extension over  .
.
If 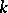 is the field of rational numbers, the problem becomes one of constructing a normal algebraic number field with given Galois group, and comes down to finding an algebraic equation over
is the field of rational numbers, the problem becomes one of constructing a normal algebraic number field with given Galois group, and comes down to finding an algebraic equation over  with the given Galois group. Such equations exist for the symmetric groups, and also for the alternating groups. I. Schur constructed equations for the alternating groups; it was shown, in particular, that equations of the form
with the given Galois group. Such equations exist for the symmetric groups, and also for the alternating groups. I. Schur constructed equations for the alternating groups; it was shown, in particular, that equations of the form
 |
(partial sums of the expansion of the exponential function) have as Galois group the alternating group if  , and the symmetric group as Galois group in other cases.
, and the symmetric group as Galois group in other cases.
I.R. Shafarevich
used the arithmetical properties of algebraic number fields to show the existence of an extension of an algebraic number field with any solvable group  as Galois group. As a solution one may select a field
as Galois group. As a solution one may select a field  such that the discriminant of
such that the discriminant of  over the algebraic number field is relatively prime with any given integer, so that the number of solutions of the problem is infinite.
over the algebraic number field is relatively prime with any given integer, so that the number of solutions of the problem is infinite.
Considering the Galois groups of infinite extensions of a given field (cf. Galois topological group) makes it possible to solve the inverse problem of Galois theory in one stroke for special classes of fields: finite fields, local fields or fields of algebraic functions in one variable.
References
| [1] | N.G. [N.G. Chebotarev] Tschebotaröw, "Grundzüge der Galois'schen Theorie" , Noordhoff (1950) (Translated from Russian) |
| [2a] | I.R. Shafarevich, "On the construction of a field with a given Galois group of order 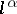 " Izv. Akad. Nauk SSSR , 18 : 2 (1954) pp. 261–296 (In Russian) " Izv. Akad. Nauk SSSR , 18 : 2 (1954) pp. 261–296 (In Russian) |
| [2b] | I.R. Shafarevich, "The construction of an algebraic number field with a given solvable Galois group" Izv. Akad. Nauk SSSR , 18 : 3 (1954) pp. 525–578 (In Russian) |
Comments
In recent years much progress has been made on the inverse problem of Galois theory over the base field  , see [a1]–[a3]. The technique is to realize first the group over the base field
, see [a1]–[a3]. The technique is to realize first the group over the base field  , the field of rational functions in one variable over the complex numbers, which is well under control. Under certain conditions on the group one can replace
, the field of rational functions in one variable over the complex numbers, which is well under control. Under certain conditions on the group one can replace 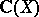 by
by 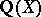 , using "descent" techniques. Finally one replaces
, using "descent" techniques. Finally one replaces 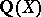 by
by 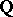 using the Hilbert irreducibility theorem (cf. Hilbert theorem). In this way many finite simple groups have been realized as Galois groups over
using the Hilbert irreducibility theorem (cf. Hilbert theorem). In this way many finite simple groups have been realized as Galois groups over 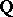 and over cyclotomic extensions of
and over cyclotomic extensions of 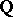 .
.
References
| [a1] | G.V. Belyi, "On extensions of the maximal cyclotomic field having a given classical Galois group" J. Reine Angew. Math. , 341 (1983) pp. 147–156 |
| [a2] | B.H. Matzat, "Konstruktive Galoistheorie" , Lect. notes in math. , 1284 , Springer (1987) |
| [a3] | J.P.Serre, "Groupes de Galois sur 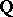 " Sem. Bourbaki , Exp. 689 (1987) " Sem. Bourbaki , Exp. 689 (1987) |
Galois theory, inverse problem of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Galois_theory,_inverse_problem_of&oldid=11544